СРЕДНИЕ ВЕЛИЧИНЫ И ИХ МЕСТО В ЭКОНОМИЧЕСКОМ АНАЛИЗЕ
Одной из обобщающих количественных характеристик является средняя величина, которая способна отразить общее, типическое, присущее всем элементам совокупности. Средние величины широко используется в планово-аналитической работе предприятий и организаций. С помощью средних величин можно дать характеристику закономерностей развития социально-экономических явлений.
Расчет средних величин является составной частью многих статистических методов (группировок, рядов динамики, индексного, выборочного, дисперсионного анализа), способ расчета и сфера применения которых определяется сущностью явления и характером исходной статистической информации.
Средняя арифметическая
Наиболеераспространенным
видом является средняя арифметическая. Она используется в тех случаях,
когда величина варьирующего признака для всей совокупности равна сумме
индивидуальных значений ее отдельных элементов. Если исходная информация
представлена в виде несгруппированных данных, рассчитывают простую среднюю
арифметическую (![]() ) по формуле:
) по формуле:
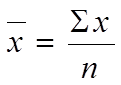 ,
(.1)
,
(.1)
где x - индивидуальные значения признака отдельных элементов совокупности (варианты); n - число этих элементов.
Когда средняя величина определяется на основе сгруппированных данных вариационного ряда распределения, необходимо использовать среднюю арифметическую взвешенную:
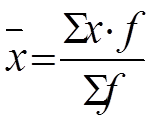 , (.2)
, (.2)
где x - варианты; f - частота их повторений.
Рассмотрим методику определения средней арифметической взвешенной на основе следующих данных.
Таблица 1.
Количество рабочих предприятия и их месячная выработка
|
Группы рабочих |
Месячная выработка, шт. x |
Количество рабочих, чел. f |
Всего
произведено изделий за месяц, шт. |
|
1 2 3 |
227 276 310 |
12 20 25 |
2724 5520 7750 |
|
Итого |
x |
57 |
15994 |
Произведение
![]() в этом
примере является экономически понятным результатом: количество произведенной за
месяц продукции. А средняя месячная выработка рабочих предприятия в отчетном
месяце составила:
в этом
примере является экономически понятным результатом: количество произведенной за
месяц продукции. А средняя месячная выработка рабочих предприятия в отчетном
месяце составила:
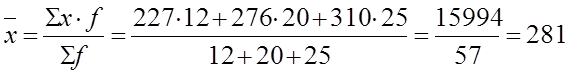
шт.
Иначе рассчитывается средняя для интервального ряда распределения. В этом случае для каждой группы определяют среднее значение интервала (х) как полусумму его границ. Ширину открытого интервала принимают равной соседнему закрытому. Приведем пример расчета средней арифметической взвешенной в интервальном ряду.
Пример:
Определить среднюю производительность труда рабочих, если известно:
Таблица .2.
Группировка рабочих по уровню месячной выработки
|
Группы рабочих по уровню месячной выработки, грн |
Количество рабочих, чел. |
|
До 200 200-300 300-400 400-500 500-600 600 и выше Всего |
2 11 24 14 8 5 64 |
Результаты расчетов сведем в таблицу .3.
Таблица 3
|
Группы рабочих по размеру выработки, грн |
Средина интервала, х |
Количество рабочих, f |
Произведено
продукции, грн |
|
До 200 200-300 300-400 400-500 500-600 600 и выше |
150 250 350 450 550 650 |
2 11 24 14 8 5 |
300 2750 8400 6300 4400 3250 |
|
Итого |
х |
64 |
25400 |
Отсюда - средняя выработка рабочих равна
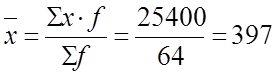
грн.
Средняя гармоническая
Если
статистические веса (частоты) в исходных данных для расчета средней величины не
даны непосредственно, а входят как сомножители в один из имеющихся показателей,
то для расчета используют формулу средней гармонической. Следовательно,
в этом случае суммированию подлежат не сами варианты, а обратные им числа ![]() .
.
Например,
затраты рабочего времени на изготовление одинаковой детали тремя рабочими
составили ![]() и
и ![]() часа, то есть
каждый из них за час изготовил соответственно 2, 3, 4 детали. Средняя из этих
чисел (средняя выработка) равна 3, а на изготовление одной детали в среднем
затрачено
часа, то есть
каждый из них за час изготовил соответственно 2, 3, 4 детали. Средняя из этих
чисел (средняя выработка) равна 3, а на изготовление одной детали в среднем
затрачено ![]() часа. Именно
такой результат получим без промежуточных вычислений, используя формулу простой
средней гармонической:
часа. Именно
такой результат получим без промежуточных вычислений, используя формулу простой
средней гармонической:
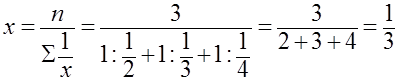 часа (3)
часа (3)
В
практической работе чаще всего используется средняя гармоническая
взвешенная. По сути, это преобразованная средняя арифметическая взвешенная
(![]() ). Ее
используют, когда показатель статистического веса (f) отсутствует и его
следует дополнительно определить на основе известных вариант (x) и
произведения вариант на частоту (
). Ее
используют, когда показатель статистического веса (f) отсутствует и его
следует дополнительно определить на основе известных вариант (x) и
произведения вариант на частоту (![]() ). Обозначив
произведение (
). Обозначив
произведение (![]() ) через (M),
получим формулу средней гармонической взвешенной:
) через (M),
получим формулу средней гармонической взвешенной:
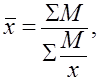 (4)
(4)
Рассчитаем среднюю урожайность озимой пшеницы, используя данные табл. .4.
Таблица 4.
Урожайность и валовой сбор озимой пшеницы сельскохозяйственного предприятия
|
Бригада |
Средняя урожайность, ц/га x |
Валовой
сбор, ц М= |
|
Первая Вторая |
40,0 45,5 |
16000 27300 |
|
Итого |
х |
43300 |
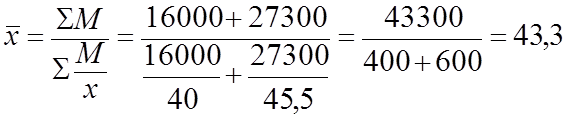 ц/га
ц/га
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.