Материалы для строительных металлических конструкций. Нормативные и расчетные сопротивления сталей, страница 14

Схема стержня	l1/l	При отношении Jmin/Jmax, равном
		0,01	0,1	0,2	0,4	0,6	0,8	1,0
	-	-	1,35	1,24	1,14	1,08	1,02	1,00
	-	-	1,66	1,45	1,24	1,14	1,06	1,00
	0,0	1,69	1,35	1,25	1,14	1,08	1,03	1,00
	0,2	1,45	1,22	1,15	1,08	1,05	1,02	-
	0,4	1,23	1,11	1,07	1,04	1,02	1,01	-
	0,6	1,07	1,03	1,02	1,01	1,01	1,00	-
	0,8	1,01	1,00	1,00	1,00	1,00	1,00	-

Расчет и конструирование

Переходим к выбору конструктивной (расчетной) схеме опоры в ее плоскости.

Определить несущую способность центрально-сжатой решетчатой стрелы четырехгранного  сечения. Пояса выполнены из уголков ∟63×5 с (А₁= 6,13 см²; z_о= 1,74 см; i_min= 1,25 см); решетка из уголков  56×4 с (А₁ = 4,38 см²).

Материал конструкций – сталь с 245 с (R_y= 24 кН/см²).

Коэффициент усилий работы γ_с = 1 (см. рис.).

Рис. 18. К расчету стрелы крана

Определим расчетные длины рабочей       стрелы в плоскости и из плоскости подвеса, пользуясь в помощь таблицей 7.

В плоскости подвеса (относительно оси Х-Х) стрела соединена с опорной конструкцией и с оттяжкой шарнирно, поэтому μ =1. Для определения коэффициента μ_f предварительно находим  (min, max) моменты инерции по формуле:

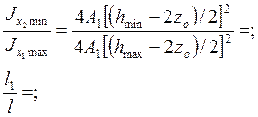
По линейной интерполяции значений таблицы 7 определяем μ₁= 1,02. Для определения расчетной длины стрелы из плоскости подвеса (относительно оси У-У) не имеем достаточных материалов для точного расчета конструкции, которые можно найти только в специальной литературе, поэтому определяем ее приблизительно, но с необходимым запасом несущей способности элементов и конструкции в целом.

При определении коэффициента μ не будем учитывать поддерживающего влияния оттяжки, принимая μ = 2; при определении коэффициента μ₁ будем рассматривать стрелу как пирамидальный стержень (центрально-сжатой решетчатой), то есть пользоваться данными второй строки таблицы 7.

Длина стрелы в плоскости подвеса по формуле:

Из плоскости подвеса имеем отношение моментов инерции по формуле:

при μ₁ = 1,66 определяем длину l_o,y по формуле:

Гибкости в плоскости и из плоскости подвеса будут равны:

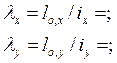
При столь большой разнице гибкостей заранее известно, что приведенная гибкость оси У-У также будет значительно больше, поэтому ограничимся расчетом только относительно этой оси.

Коэффициент φ_b найдем в функции гибкости ветви:

Приведенную гибкость стрелы, условную гибкость и коэффициент φ определим по формулам

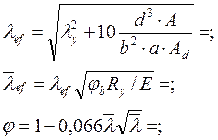
Несущую способность рабочей стрелы вычисляем по формуле:

Обращаем особое внимание на то что мы рассматриваем стрелу как центрально-сжатый стержень.

Это можно делать только при малых значениях моментов от ветровой нагрузки и собственного веса сравнительно с продольной силой.

Критерии таких оценок будут даны при рассмотрении работы сжато-изгибаемых элементов.

Значения расчетных данных стрелы крана

Таблица 8

Параметры конструирования	lo,x, м	lo,y, м	λх	λу	λb	λef	N
Расчетные параметры для рабочей стрелы

Контрольные вопросы

1.  Что такое коэффициент условий работы γ_с?