Расчет сечений изгибаемых элементов. Центрально и внецентренно сжатые элементы при реконструкции производственного здания, страница 16

Решение

Для более наглядного представления рассмотрим (вспомним) распределение давления под балкой на опоре и определения расчетного пролета.

Рис. 9. Схема распределения давления под балкой

где l_оп – длина опорного участка балки

Силу давления балки на опору F будем считать приложенной в одной точке – центр опорной поверхности. Р – равномерно распределено по всей опорной поверхности, на самом деле практически оно передается неравномерно, но это трудно учесть (в условиях лаборатории).

Рис. 10. Схема определения расчетного пролета

Расстояния между серединами опорных участков считается расчетной длиной балки l_оили расчетным пролетом

где l – расстояние между разбивочными осями;

l_св – расстояние между опорами в свету;

l_о– расчетный пролет;

l_оп – опорный участок;

δ – расстояние от оси до края элемента

Далее студент самостоятельно составляет расчетные схемы по указанной ниже конструктивной схеме. Считая, что расчетная схема опоры соответствует конструктивной при принятых упрощениях.

Рис. 11. Схема шарнирно- подвижной опоры

б) расчетная схема

выполняет студент

1 – балка до приложения силы F; 2 – балка после приложения силы F;

3 – шарнир; 4 – опорный стержень

Изображенная расчетная схема правой опорой должна соответствовать конструктивной и по геометрическим признакам, так как опорный стержень препятствует только вертикальному перемещению, и по статическим признакам, так как возникает единственная реакция по направлению опорного стержня.

Рис. 12. Схема шарнирно-неподвижной опоры

а) конструктивная схема

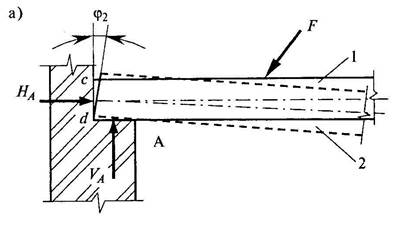
б) расчетная схема

выполняет студент

1 – балка до приложения силы F; 2 – балка после приложения силы F;

3 – шарнир; 4 – опорные стержни

Расчетная схема опоры А должна быть представлена с точки зрения геометрии такая опора характерна тем, что препятствует вертикальному и горизонтальному перемещениям и допускает поворот сечения C-d на опоре на некоторый угол φ₂.

По статике такая опора должна характеризоваться возникновением двух составляющих реакций. Возникает  одна наклонная реакция, которую для удобства расчетов нужно представлять в виде двух составляющих.

Рис. 13. Схема простой балки

а) конструктивная схема простой балки

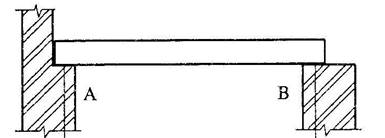
б) расчетная  схема

выполняет студент

в) расчетная  схема

выполняет студент

Требуется представить шарнирно-неподвижная опора. Оба варианта можно изобразить; опоры равноценны как с геометрической, так и со статической точки зрения.

Лабораторный          

практикум

2 часа                                                

Схемы работы балок с консольными участками и балок- консолей

По изученным и исследованным ранее материалам самостоятельно продолжить построение рассчитанных схем в соответствии задания.

Рис. 14. Схема опирания балки на кирпичные стены

а) фактическая схема

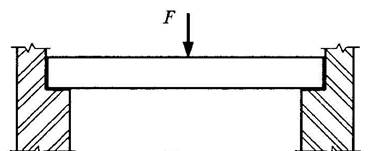
б) деформационная  схема

в) расчетная реальная   схема

выполняет студент

г) расчетная  схема, принимаемая для расчета

выполняет студент

Если исходить из принятых выше обозначений опор, то такая балка должна иметь две шарнирные неподвижные опоры. В реальных балочных конструкциях при таком опирании под действием нагрузки в результате деформации балки расстояние между ее концами уменьшается, не встречая сопротивления опор горизонтальным перемещениям концов балки (если нет специальных устройств, препятствующих этому перемещению).

Консольные балки – балки, у которых один конец жестко прикреплен к основанию (жесткая заделка), а другой свободен, называется консолью.

Рис. 15. Балка с консольным участком

а) конструктивная    схема

б) расчетная  схема

выполняет студент

Балка на двух опорах может иметь один конец свободный, тогда участок балки длиной а, расположенный за опорой, называется консольным. Расчетная схема  такой балки для сравнительно коротких балок. Для большепролетных балок и ферм, например, мостовые опоры, устраиваются иначе.

Рис. 16. Схема консоли

а) конструктивная    схема

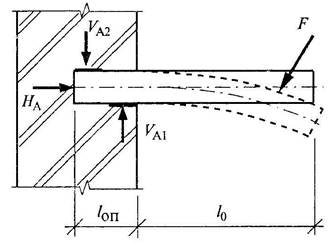
б) расчетная   схема

выполняет студент