Численное дифференцирование. Разработка алгоритмов и проектировка программного обеспечения для решения дифференциальных уравнений в частных производных

МИНИСТЕРСТВО ОБРАЗОВАНИЯ РЕСПУБЛИКИ БЕЛАРУСЬ

УЧРЕЖДЕНИЕ ОБРАЗОВАНИЯ

«ГОМЕЛЬСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ ИМЕНИ П. О. СУХОГО»

Кафедра «Информационные технологии»

Лабораторная работа №5

по дисциплине: «Численные методы математической физики»

на тему: «Численное дифференцирование»

Выполнил студент гр. ИТ-31

Принял преподаватель

Гомель 2015

Цель работы: Научиться разрабатывать алгоритмы и проектировать программное обеспечение для решения дифференциальных уравнений в частных производных. 

Ход работы

Задание 1

Решить ДУЧП нестационарной задачи теплопроводности, используя явную и неявную двухслойную схему метода конечных разностей. Начальные и граничные условия, а также правая часть дифференциального уравнения приведены в таблице. Величины L и T задать самостоятельно. Построить трехмерный график искомой функции u(x,t) для области 0<x<L и 0<t<T. 

Вариант 9

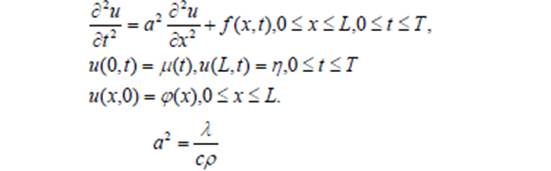
Граничные условия          Начальные условия u(x,0)

u(0,t) -> sin(t–8)                 u(х,0) ->

   Исходный код программы:

Явная схема:

function y=myu(t)

y=sin(t-8)

endfunction

function y=fi(x)

y=(x*x-4*x+3)^(1/3);

endfunction

function [u, x, t]=parabol(N, K, L, T, a)

h=L/N;

delta=T/K;

for i=1:N+1

x(i)=(i-1)*h;

u(i,1)=fi(x(i));

end

for j=1:K+1

t(j)=(j-1)*delta;

u(1,j)=myu(t(j));

u(N+1,j)=0;

end

gam=a^2*delta/h^2;

for j=1:K

for i=2:N

u(i,j+1)=gam*u(i-1,j)+(1-2*gam)*u(i,j)+gam*u(i+1,j);

end

end

endfunction

[U,X,T]=parabol(50,200,5,3,0.4);

plot3d(X,T,U);

title(’PARABOLIC EQUATION’);

xlabel(’X’);

ylabel(’T’);

Неявная схема:

function y=myu(t)

y=sin(t-8)

endfunction

function y=fi(x)

y=(x*x-4*x+3)^(1/3);

endfunction

function [u, x, t, r, k]=neyavn(N, K, L, T, a, eps)

h=L/N;

delta=T/K;

for i=1:N+1

x(i)=(i-1)*h;

u(i,1)=fi(x(i));

end

for j=1:K+1

t(j)=(j-1)*delta;

u(1,j)=myu(t(j));

u(N+1,j)=0;

end

R(N+1,K+1)=0;

gam=a^2*delta/h^2;

r=1;

k=0;

while r>eps

for i=2:N

for j=2:K+1

R(i,j)=abs(u(i,j)-gam/(1+2*gam)*(u(i-1,j)+u(i+1,j))-u(i,j-1)/(1+2*gam));

u(i,j)=gam/(1+2*gam)*(u(i-1,j)+u(i+1,j))+u(i,j-1)/(1+2*gam);

end

end

r=R(1,1);

for i=1:N+1

for j=1:K+1

if R(i,j)>r

r=R(i,j);

end

end

end

k=k+1;

end

endfunction

[U,X,T]=neyavn(50,200,5,3,0.4,0.1);

plot3d(X,T,U);

title('PARABOLIC EQUATION');

xlabel('X');

ylabel('  T');

zlabel('U')

Результат выполнения программы явной схемы представлен на рисунке 1.

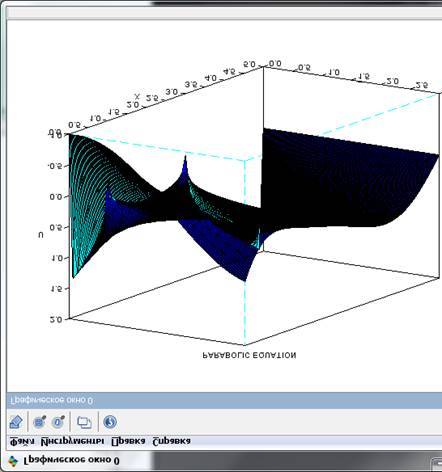
Рисунок 1 – График полученных значений

Результат выполнения программы неявной схемы представлен на рисунке 2.

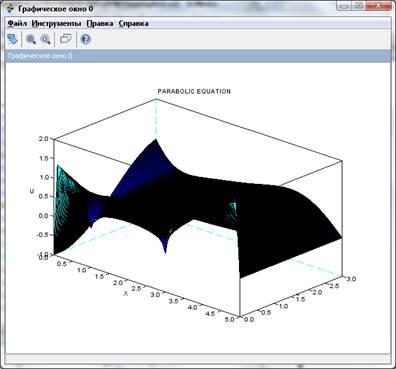
Рисунок 2 – График полученных значений

Вывод: в ходе выполнения лабораторной работы были построены графики с использованием явной и неявной схемы по методу конечных разностей. При вычислениях были учтены все начальные и граничные условия.