int splitCount = (currentArgs->end - currentArgs->start) / currentArgs->dx;
for (size_t j = 0; j < splitCount; j++)
{
x = currentArgs->start + currentArgs->dx * j;
WAIT(currentArgs->bLock, 1);
for (size_t i = 0; i < 1000; i++)
{
long double igrek = 0;
for (size_t k = 1; k < i; k++)
{
igrek += exp(currentArgs->bufferBeta[i] / 100.0);
}
currentArgs->bufferIgrek[i] = igrek;
}
FREE(currentArgs->yLock, 0);
}
return 0;
}
unsigned int _stdcall IntegralSolver::ThreadCalculateGamma(void* pParam)
{
Args* currentArgs = static_cast<Args*>(pParam);
double x;
int splitCount = (currentArgs->end - currentArgs->start) / currentArgs->dx;
for (size_t j = 0; j < splitCount; j++)
{
x = currentArgs->start + currentArgs->dx * j;
WAIT(currentArgs->yLock, 1);
for (size_t i = 0; i < 1000; i++)
{
double gamma = 0;
for (size_t k = 1; k < i; k++)
{
gamma += sin(x * 3.14 / 180) * cos(currentArgs->bufferIgrek[i] * 3.14 / 180.0);
}
currentArgs->bufferGamma[i] = gamma;
}
FREE(currentArgs->gLock, 0);
}
return 0;
}
unsigned int _stdcall IntegralSolver::ThreadCalculateFunction(void* pParam)
{
Args* currentArgs = static_cast<Args*>(pParam);
double x;
int splitCount = (currentArgs->end - currentArgs->start) / currentArgs->dx;
for (size_t j = 0; j < splitCount; j++)
{
x = currentArgs->start + currentArgs->dx * j;
if (x <= -1)
{
currentArgs->bufferFunc[j] = 0;
}
else
{
double sumFirstBlock = 0;
double sumSecondBlock = 0;
double sumThirdBlock = 0;
WAIT(currentArgs->gLock, 1);
for (size_t i = 0; i < 1000; i++)
{
sumFirstBlock += currentArgs->bufferAlpha[i];
sumSecondBlock += currentArgs->bufferBeta[i];
sumThirdBlock += currentArgs->bufferGamma[i];
}
currentArgs->bufferFunc[j] = log(1 + x) * (sumFirstBlock + sumSecondBlock + sumThirdBlock);
}
FREE(currentArgs->funcLock, 0);
}
return 0;
}
unsigned int _stdcall IntegralSolver::ThreadCalculateIntegral(void* pParam)
{
Args* currentArgs = static_cast<Args*>(pParam);
double x;
int splitCount = (currentArgs->end - currentArgs->start) / currentArgs->dx;
for (size_t j = 0; j < splitCount; j++)
{
x = currentArgs->start + currentArgs->dx * j;
WAIT(currentArgs->funcLock, 1);
WaitForSingleObject(*(currentArgs->mutex), INFINITE);
fprintf(currentArgs->file, "\n\tx = %.3f\t\tf(%.3f) = %.3f\n", x, x, currentArgs->bufferFunc[j]);
for (size_t i = 0; i < 1000; i++)
{
fprintf(currentArgs->file, "\t\ta%d = %.3f\tb%d = %.3f\tg%d = %.3f\n",
i, currentArgs->bufferAlpha[i],
i, currentArgs->bufferBeta[i],
i, currentArgs->bufferGamma[i]
);
}
ReleaseMutex(*(currentArgs->mutex));
FREE(currentArgs->startLock, 0);
}
double square = 0;
for (size_t j = 0; j < splitCount - 1; j++)
{
square += (currentArgs->bufferFunc[j] + currentArgs->bufferFunc[j + 1]) * currentArgs->dx / 2;
}
*(currentArgs->answer) = square;
SetEvent(*(currentArgs->isSolved));
return 0;
}
void IntegralSolver::SetFileName(char* filename)
{
file = fopen(filename, "w+");
}
void IntegralSolver::GetAnswer(Args* myArgs)
{
fprintf(myArgs->file, "Результаты вычислений на отрезке [%.3f;%.3f] с шагом %.4f",
myArgs->start, myArgs->end, myArgs->dx);
_beginthreadex(NULL, 0, &IntegralSolver::ThreadCalculateAlpha, myArgs, 0, NULL);
_beginthreadex(NULL, 0, &IntegralSolver::ThreadCalculateBeta, myArgs, 0, NULL);
_beginthreadex(NULL, 0, &IntegralSolver::ThreadCalculateIgrek, myArgs, 0, NULL);
_beginthreadex(NULL, 0, &IntegralSolver::ThreadCalculateGamma, myArgs, 0, NULL);
_beginthreadex(NULL, 0, &IntegralSolver::ThreadCalculateFunction, myArgs, 0, NULL);
_beginthreadex(NULL, 0, &IntegralSolver::ThreadCalculateIntegral, myArgs, 0, NULL);
ReleaseMutex(*(myArgs->mutex));
}
Тесты:

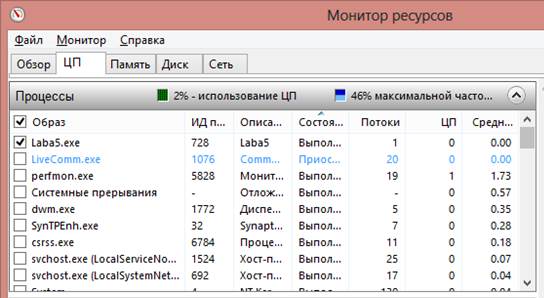
Рис. 1 Потоки до нажатия кнопки рассчитать
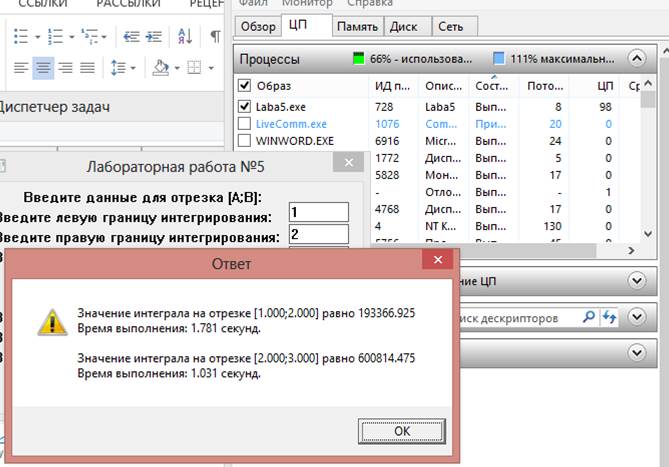
Рис. 2 Потоки до нажатия кнопки рассчитать
Выводы: В ходе лабораторной работы была разработана программа, осуществляющая решение поставленной задачи с помощью многопоточного приложения
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.