pzmap(w_p2); %..Карта_полюсов_придаточной_функции_w_p2
title('Карта полюсов'); %..служит_для_вывода_название_графика
k1=pzmap(w_p1); %..Корни_придаточных_функции
k2=pzmap(w_p2); %..Корни_придаточных_функции
disp('Корни придаточной функции w_p1:');
disp(k1);
disp('Корни придаточной функции w_p2:');
disp(k2);

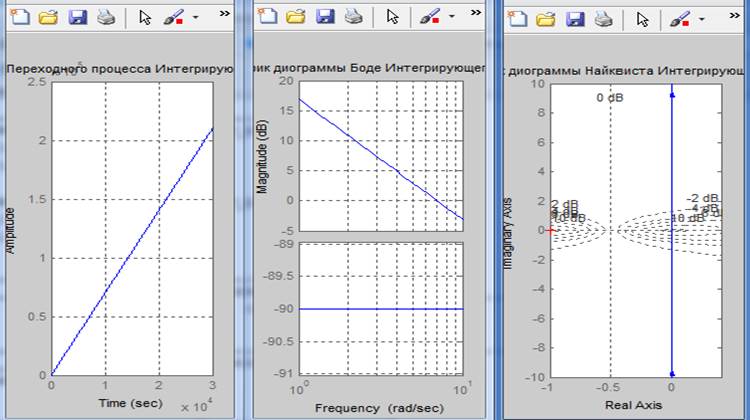
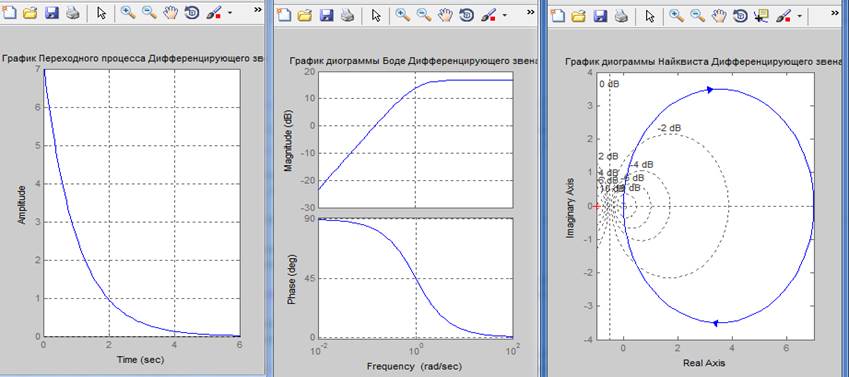
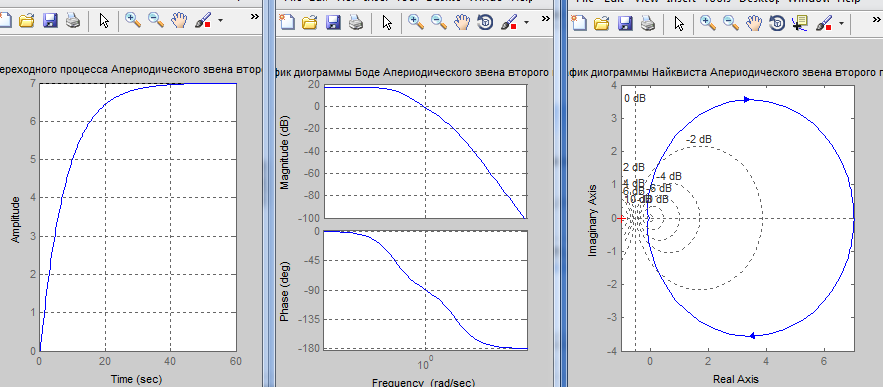
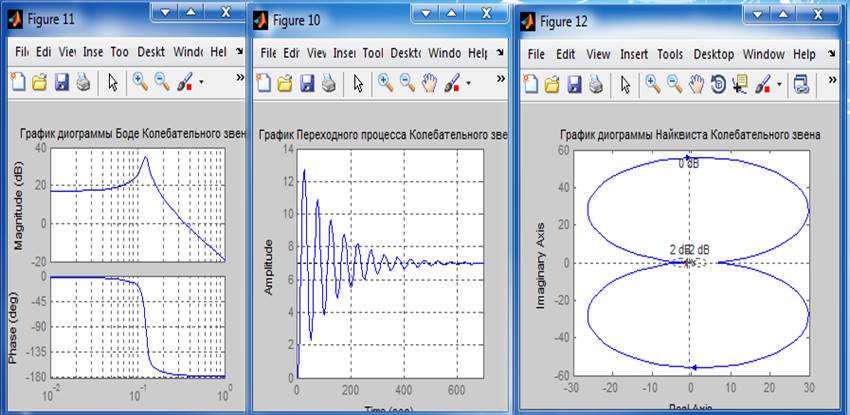
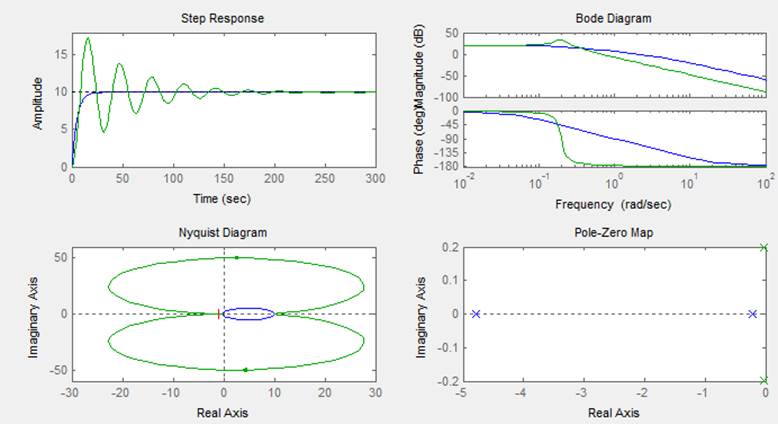
Формула, график переходной функции и карта полюсов для устойчивой системы:
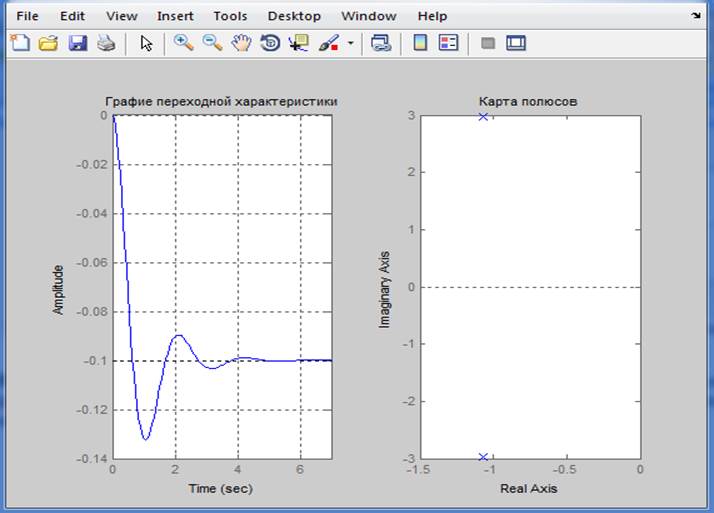
Формула, график переходной функции и карта полюсов для неустойчивой системы:
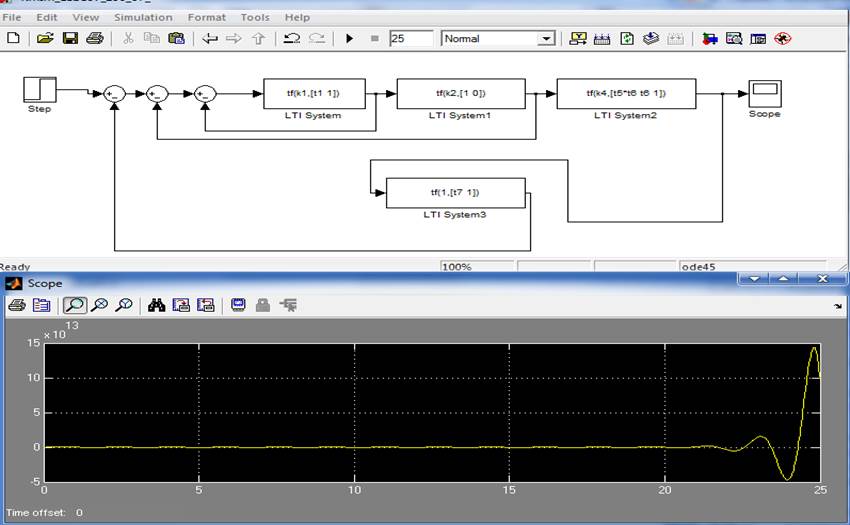
Чтобы проверить влияние параметра k на вид графика было произведено моделирование с несколькими различными значениями в результате чего, было выяснено что он не влияет на вид графика.
Листинг программы в Matlab:
KMIM_Laba_07_06_07.m
clear all; %..Очистка_перменных
close all; %..закрытие_окон
k1=7; %..Параметр_системы
k2=15; %..Параметр_системы
k3=5; %..Параметр_системы
k4=13; %..Параметр_системы
t1=0.05; %..Параметр_системы
t2=0.6; %..Параметр_системы
t3=0.15; %..Параметр_системы
t4=0.95; %..Параметр_системы
t5=0.8; %..Параметр_системы
t6=0.33; %..Параметр_системы
w1=tf([0 k1],[0 t1 1]); %..Предаточные_функции
w2=tf([0 k2],[0 1 0]); %..Предаточные_функции
w3=tf([k3*t3 t3],[0 t4 1]); %..Предаточные_функции
w4=tf([0 k4],[t5*t6 t6 1]); %..Предаточные_функции
H=feedback(series(series(w1,feedback(parallel(w2,w3),1)),w4),1);
figure(1); %..создаем_графическое_окно
clf(); %..очистка_графического_окна
step(H); %..График_переходного_процесса
title('График Переходного процесса'); %..служит_для_вывода_название_графика
grid; %..сетка
figure(2); %..создаем_графическое_окно
clf(); %..очистка_графического_окна
bode(H); %..График_диограммы_Боде
title('График диограммы Боде'); %..служит_для_вывода_название_графика
grid; %..сетка
figure(3); %..создаем_графическое_окно
clf(); %..очистка_графического_окна
nyquist(H); %..График_диограммы_Найквиста
title('График диограммы Найквиста'); %..служит_для_вывода_название_графика
grid;
p=pzmap(H);
disp('Корни придаточной функции H:');
disp(p);
figure(4); %..создаем_графическое_окно
clf(); %..очистка_графического_окна
pzmap(H); %..График_корней
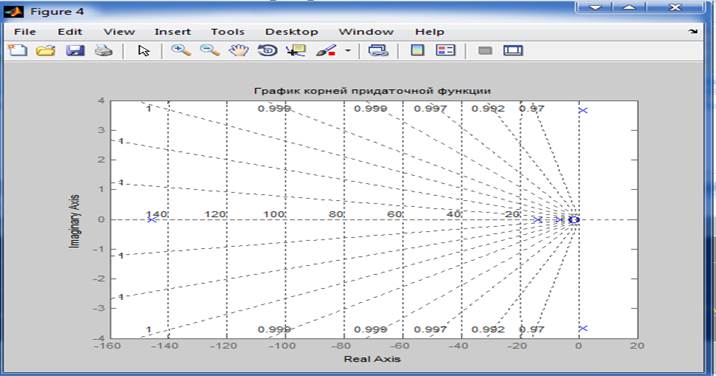
title('График корней придаточной функции'); %..служит_для_вывода_название_графика
grid;


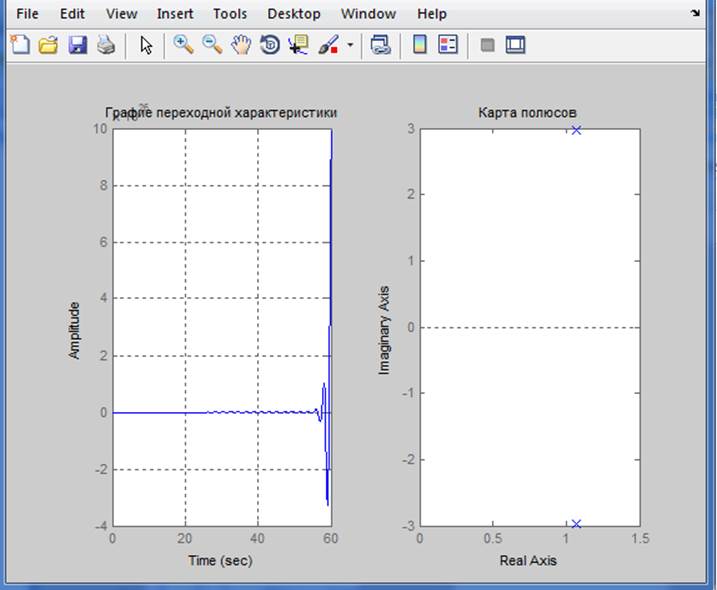
Так как в системе присутствуют корни с положительной вещественной частью, то можно сделать вывод, что система является неустойчивой. Наличие в корнях комплексной части говорит о колебательном процессе.
С=1;
K=1;
M=60;

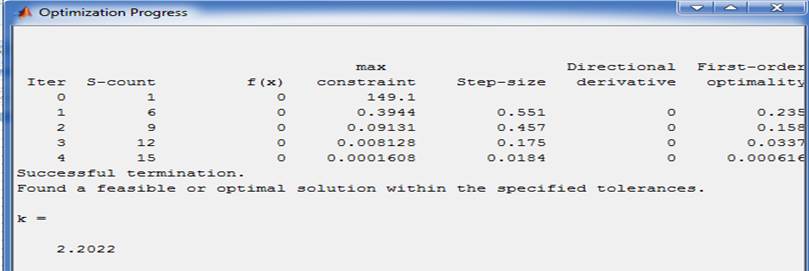
Вывод: Получили навыки моделирования САУ с использованием М-файлов и в пакете Simulink, научиться применять функции пакета Control System Toolbox для анализа моделей САУ, выполнять графическую интерпретацию полученных результатов.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.