2. Смоделируем первую составляющую в виде Sine Wave – источника синусоидального сигнала с параметрами: амплитуда – 50, частота – 5. Умножим ее на 1/m, где m можно задать числовым значением непосредственно в блоке, а можно поместить в область рабочей памяти в командном режиме перед запуском модели на выполнение, например, >>m=10
Смоделируем вторую составляющую в виде подсистемы с одним входом и одним выходом. Для этого включим в модель блок Subsystem, раскроем его и смоделируем два слогаемых, причем для моделирования интеграла используется блок Integrator.
3. Для того, чтобы найти значение v(t), нужно сложить две составляющие и проинтегрировать полученный сигнал. Следует заметить, что результат интегрирования v(t) является входным сигналом для подсистемы.
4. Задать в командном режиме для модели следующие параметры:
m=10
α=2.5
K=50
5. Задать время моделирования, равное 30с.
6. Запустить модель на обработку, получить график функции скорости v(t).
7. Добавить в модель блок Integrator для получения функции перемещения массы. Построить график функции перемещения.
Вид модели в simulink:
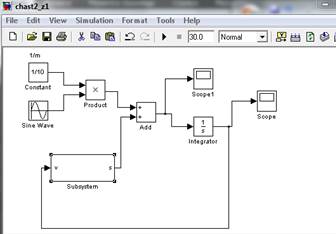
Содержание подсистемы модели:

Полученный график функции скорости:
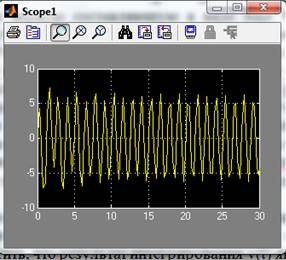
Полученный график функции перемещения:

Задача 2
Рассчитать значение функций перемещения и скорости динамической системы для индивидуального задания (папка «Задачи»). Модель задана дифференциальным уравнением второго порядка. Построить графики выходных параметров модели, для этого:
1. Создать блочную модель системы в Simulink
2. Запустить модель на выполнение, получить графики перемещения, скорости механической системы.
3. Оформить модель как подсистему
Исходными данными для задачи являются:
• К -жесткость пружины.
• m - масса груза.
• α - коэффициент демпфирования.
• F0 - амплитуда возмущающей силы.
• w - частота возмущающей силы.
• Т – время исследования системы
Таблица 2.1 - Таблица исходных данных
|
N |
m, кг |
К КН/м |
α КН/м/с |
F0 КН |
w c-1 |
Т с |
|
1 |
10 |
50 |
2,5 |
4 |
50 -150 |
40 |
Описание математической модели
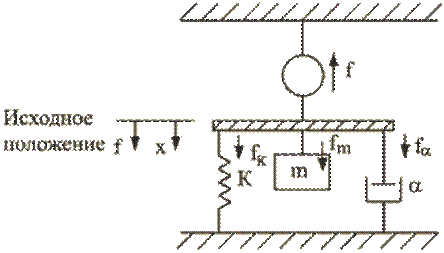
На рисунке представлена механическая система с
пружиной и демпфером. Она содержит массу ![]() , связанную с
пружиной
, связанную с
пружиной ![]() : на них
действуют сила трения
: на них
действуют сила трения ![]() и внешняя сила
и внешняя сила ![]() .
.
Интегро-дифференциальное уравнение, которому подчиняется движение системы, получим, используя принцип Д'Аламбера. Уравнение сил
![]()
можно записать в виде:
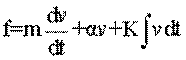 .
где
.
где ![]() -
перемещение от положения свободного равновесия; v - скорость движения
системы.
-
перемещение от положения свободного равновесия; v - скорость движения
системы.
Данное интегро-дифференциальное уравнение можно преобразовать в дифференциальное уравнение вида:

F(t) = F0sin(wt) – возмущающая сила, действующая на систему.
Вид блока основной модели в Simulink:

Вид подсистемы Subsystem и Subsystem1:
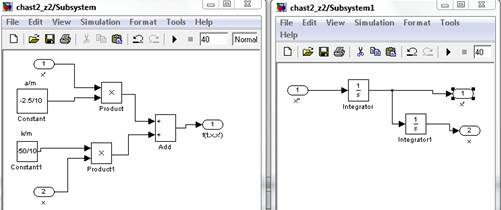
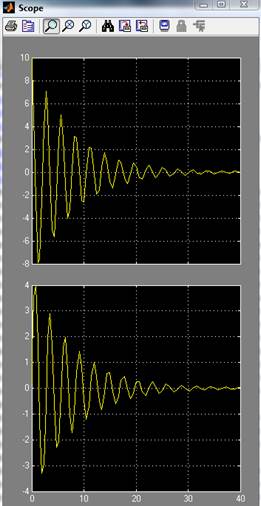
График функций перемещения и скорости движения груза:
Задача 3
Разработать передаточную функцию для модели задачи 2. Произвести расчет выходных параметров по модели с использованием передаточной функции, для чего:
1. Создать блочную модель системы в Simulink
2. Запустить модель на выполнение, получить графики перемещения, скорости механической системы.
3. Оформить модель как подсистему
4. Вывести на одном графике результаты моделирования задач 2 и 3, сравнить их.
Вид подсистемы Subsystem и Subsystem1:
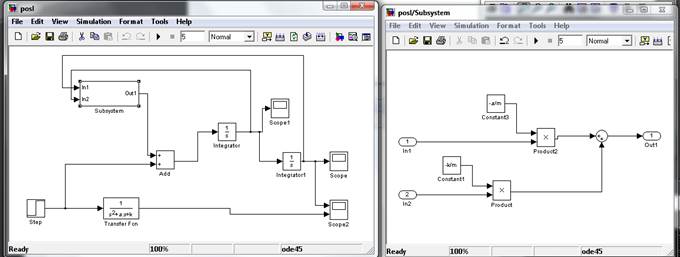
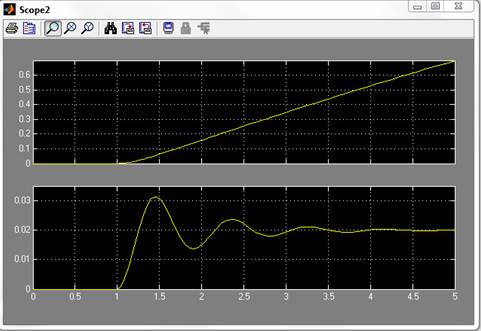
График функций перемещения и скорости движения груза:


График функций перемещения и передаточная функция движения груза:
Выводы : во время выполнения лабораторной работы получили навыки построения блочных моделей в пакете Simulink, научились выполнять графическую интерпретацию полученных результатов, формировать входные сигналы различной формы и производить операции над ними; получили навыки создания пользовательских моделей для визуального моделирования систем, описываемых интегро-дифференциальными и дифференциальных уравнениями.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.