



























































МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ
РЯЗАНСКАЯ ГОСУДАРСТВЕННАЯ РАДИОТЕХНИЧЕСКАЯ АКАДЕМИЯ
, ,
,
СБОРНИК ЗАДАЧ
ПО ЭЛЕКТРОДИНАМИКЕ
Рязань 2005
Министерство образования и науки Российской Федерации
Рязанская государственная радиотехническая академия
, ,
,
СБОРНИК ЗАДАЧ
ПО ЭЛЕКТРОДИНАМИКЕ
Учебное пособие
Рязань 2005
УДК 538.3
Сборник задач по электродинамике: Учеб. пособие / А.И.Бакулин, Б.В.Кагаленко, Н.И.Шамеева, Г.Г.Юмашева; Рязан. гос. радиотехн. акад. Рязань, 2005. 80 с. ISBN 5-7722-0076-3.
Настоящее учебное пособие дополняет лекционный материал по курсу "Электродинамика и распространение радиоволн". Содержит двенадцать разделов, представленных задачами, а также соответствующими формулами и определениями.
В разделе "Приложения" даны основные единицы измерения физических величин по международной системе единиц (СИ), классификация электромагнитных волн, сводка применений дифференциального оператора, корни функций Бесселя, приведены ответы и библиографический список.
Предназначено для студентов дневной и вечерней форм обучения специальностей 200700, 201000, 201200, 201600, 230200.
Табл. 9. Ил. 67. Библиогр.: 7 назв.
Электродинамика, поле, волновод, резонатор, вибратор
Печатается по решению редакционно-издательского совета Рязанской государственной радиотехнической академии.
Рецензент: кафедра РУС Рязанской государственной радиотехнической академии (зав. кафедрой проф. С.Н.Кириллов)
Б а к у л и н Анатолий Иванович
К а г а л е н к о Борис Васильевич
Ш а м е е в а Нелли Измайловна
Ю м а ш е в а Галина Гавриловна
Сборник задач по электродинамике
Редактор Р.К. Мангутова
Корректор С.В.Макушина
Подписано в печать 26.04.05. Формат бумаги 60х84 1/16.
Бумага газетная. Печать трафаретная. Усл. печ. л. 5,0.
Уч.-изд. л. 5,0. Тираж 150 экз. Заказ
Рязанская государственная радиотехническая академия.
390005, Рязань, ул. Гагарина, 59/1.
Редакционно-издательский центр РГРТА.
ISBN 5-7722-0076-3 © Рязанская государственная радиотехническая академия, 2005
ПРИНЯТЫЕ ОБОЗНАЧЕНИЯ
Обозначение координат и единичных векторов
![]() - декартовы координаты;
- декартовы координаты;
![]() - единичные
векторы в декартовых координатах;
- единичные
векторы в декартовых координатах;
![]() -
цилиндрические координаты;
-
цилиндрические координаты;
![]() - единичные
векторы в цилиндрических координатах:
- единичные
векторы в цилиндрических координатах:
![]() - сферические
координаты;
- сферические
координаты;
![]() - единичные векторы
в сферических координатах.
- единичные векторы
в сферических координатах.
Обозначения величин
![]() - векторный потенциал поля;
- векторный потенциал поля;
![]() - магнитная индукция, Тл;
- магнитная индукция, Тл;
![]() - электрическая емкость, Ф;
- электрическая емкость, Ф;
![]() - скорость света (3×108 м/с);
- скорость света (3×108 м/с);
![]() - электрическое смещение, Кл/м2;
- электрическое смещение, Кл/м2;
![]() - напряженность электрического поля, В/м;
- напряженность электрического поля, В/м;
![]() - электродвижущая сила, В;
- электродвижущая сила, В;
![]() - частота, Гц;
- частота, Гц;
![]() - напряженность магнитного поля, А/м;
- напряженность магнитного поля, А/м;
![]() - сила тока, А;
- сила тока, А;
![]() - объемная плотность тока, А/м2;
- объемная плотность тока, А/м2;
![]() - поверхностная плотность тока, А/м;
- поверхностная плотность тока, А/м;
![]() - линейная плотность тока, А;
- линейная плотность тока, А;
![]() - индуктивность, Гн;
- индуктивность, Гн;
![]() - взаимная индуктивность, Гн;
- взаимная индуктивность, Гн;
![]() -мощность,
Вт;
-мощность,
Вт;
![]() - добротность;
- добротность;
![]() - объемная плотность заряда, Кл/м3;
- объемная плотность заряда, Кл/м3;
![]() - поверхностная плотность заряда, Кл/м2;
- поверхностная плотность заряда, Кл/м2;
![]() - линейная плотность заряда, Кл/м;
- линейная плотность заряда, Кл/м;
![]() - радиус-вектор;
- радиус-вектор;
![]() - текущее значение paдиyca в
сферической системе координат;
- текущее значение paдиyca в
сферической системе координат;
![]() - электрическое сопротивление, Ом;
- электрическое сопротивление, Ом;
![]() - удельное поверхностное сопротивление, Ом;
- удельное поверхностное сопротивление, Ом;
![]() - период, с;
- период, с;
![]() - время, с;
- время, с;
![]() - электрическое
напряжение, разность потенциалов, В;
- электрическое
напряжение, разность потенциалов, В;
![]() - фазовая скорость электромагнитной волны, м/с;
- фазовая скорость электромагнитной волны, м/с;
![]() - групповая скорость электромагнитной волны, м/с;
- групповая скорость электромагнитной волны, м/с;
![]() - энергия, Дж;
- энергия, Дж;
![]() - волновое сопротивление, Ом;
- волновое сопротивление, Ом;
![]() - характеристическое сопротивление, Ом;
- характеристическое сопротивление, Ом;
![]() - коэффициент затухания, 1/м;
- коэффициент затухания, 1/м;
![]() - коэффициент фазы, 1/м;
- коэффициент фазы, 1/м;
![]() - удельная проводимость, См/м;
- удельная проводимость, См/м;
![]() - диэлектрическая проницаемость (относительная);
- диэлектрическая проницаемость (относительная);
![]() - электрическая постоянная (1/120
- электрическая постоянная (1/120![]() ), Ф/м;
), Ф/м;
![]() - абсолютная диэлектрическая проницаемость, Ф/м;
- абсолютная диэлектрическая проницаемость, Ф/м;
![]() - длина волны, м;
- длина волны, м;
![]() - длина волны в волноводе, м;
- длина волны в волноводе, м;
![]() - магнитная проницаемость (относительная);
- магнитная проницаемость (относительная);
![]() - магнитная постоянная (120
- магнитная постоянная (120![]() /с), Гн/м;
/с), Гн/м;
![]() - абсолютная магнитная проницаемость, Гн/м;
- абсолютная магнитная проницаемость, Гн/м;
![]() - коэффициент
распространения волны, 1/м;
- коэффициент
распространения волны, 1/м;
![]() - вектор Пойнтинга, Вт/м2;
- вектор Пойнтинга, Вт/м2;
Ф - магнитный поток, Вб;
![]() - потенциал
(скалярный), В;
- потенциал
(скалярный), В;
![]() - магнитное потокосцепление, Вб;
- магнитное потокосцепление, Вб;
![]() - круговая частота, рад/с;
- круговая частота, рад/с;
![]() - коэффициенты отражения;
- коэффициенты отражения;
![]() - коэффициенты прохождения.
- коэффициенты прохождения.
1. ВЕКТОРЫ
Некоторые формулы векторной алгебры
Скалярное произведение векторов ![]() и
и ![]() :
:
![]() , где
, где
![]() - угол между направлениями
- угол между направлениями ![]() и
и ![]() .
.
Векторное произведение векторов ![]() и
и ![]()
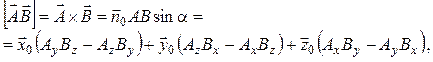
где ![]() - единичный вектор нормали к плоскости векторов
- единичный вектор нормали к плоскости векторов ![]() и
и ![]() , причем
, причем ![]() ,
, ![]() и
и ![]() образуют «правую
тройку» векторов.
образуют «правую
тройку» векторов.
В краткой записи
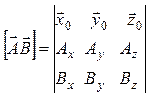 .
.
Векторное
произведение некоммутативно ![]() .
.
Векторно-скалярное (смешанное) произведение ![]() ,
, ![]() и
и ![]()
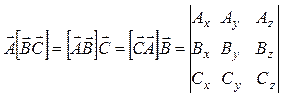 .
.
Двойное векторное произведение векторов ![]() ,
, ![]() и
и ![]()
![]() .
.
Операции векторного анализа
Для математического описания физического состояния точек пространства вводят понятия скалярных и векторных полей.
Одной из
характеристик скалярного поля ![]() является
градиент (
является
градиент (![]() ) - вектор,
показывающий величину и направление наибыстрейшего возрастания скалярного поля.
) - вектор,
показывающий величину и направление наибыстрейшего возрастания скалярного поля.
Направление градиента всегда перпендикулярно к эквипотенциальной поверхности (поверхности равного уровня) и параллельно касательной к силовой линии поля в данной точке.
В декартовой системе координат
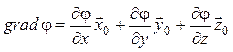 .
.
Дифференциальными характеристиками векторного поля ![]() являются скалярная
величина - дивергенция (
являются скалярная
величина - дивергенция (![]() ) и векторная величина
- ротор (
) и векторная величина
- ротор (![]() ).
).
Значение дивергенции равно плотности источников рассматриваемого поля в заданной точки пространства.
Дивергенцию векторного поля ![]() вычисляют путем дифференцирования
его проекций по соответствующим координатам.
вычисляют путем дифференцирования
его проекций по соответствующим координатам.
В декартовой системе координат
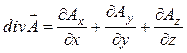 , в цилиндрической системе
, в цилиндрической системе
![]() , в сферической системе координат
, в сферической системе координат
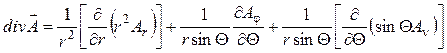 .
.
В декартовой системе координат
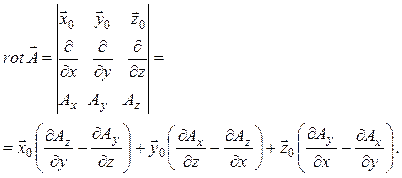
Если ![]() =0, то поле является потенциальным. Векторное поле
=0, то поле является потенциальным. Векторное поле ![]() , удовлетворяющее во
всех точках рассматриваемой области условию
, удовлетворяющее во
всех точках рассматриваемой области условию ![]() =0, называется соленоидальным.
=0, называется соленоидальным.
Соответствующими интегральными характеристиками векторного
поля являются поток через замкнутую поверхность и циркуляция вектора ![]() .
.
Потоком вектора ![]() сквозь замкнутую поверхность
сквозь замкнутую поверхность
![]() называется интеграл вида
называется интеграл вида ![]() .
.
Циркуляцией вектора ![]() по замкнутому
контуру
по замкнутому
контуру ![]() независимо от физического смысла вектора
независимо от физического смысла вектора ![]() называется интеграл
вида
называется интеграл
вида ![]() .
.
Поток и циркуляция - величины скалярные. В частном случае, когда вектор ![]() имеет смысл вектора
силы, указанный интеграл выражает работу силы по контуру
имеет смысл вектора
силы, указанный интеграл выражает работу силы по контуру ![]() .
.
Дифференциальные операции со скалярными и векторными полями
удобно записывать с помощью оператора Гамильтона ![]() . Применительно
к скалярному полю
. Применительно
к скалярному полю ![]() ;
относительно векторного поля
;
относительно векторного поля ![]() ,
, ![]() .
.
Из дифференциальных операций второго порядка в
электродинамике часто используется оператор Лапласа ![]() . Для скалярного поля
. Для скалярного поля
![]() , для векторного поля
, для векторного поля ![]() .
.
Оператор Лапласа в различных координатных системах записывается следующим образом: в декартовой системе
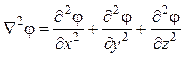 , в цилиндрической системе
, в цилиндрической системе
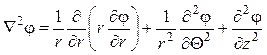 , в сферической системе координат
, в сферической системе координат
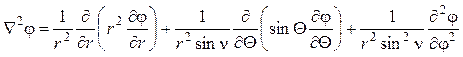 .
.
Графически векторные поля изображают с помощью силовых линий. В каждой точке силовой линии вектор поля касателен к ней. Густота силовых линий соответствует интенсивности поля. Дифференциальное уравнение силовых линий в декартовой системе координат имеет вид:
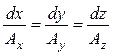 .
.
Для решения задач векторного анализа часто бывает
удобно пользоваться формулой Грина 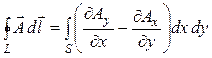 , теоремой Стокса
, теоремой Стокса ![]() , теоремой Остроградского-Гаусса
, теоремой Остроградского-Гаусса ![]() .
.
Задачи
1.1.
Найти сумму и разность
двух векторов ![]() и
и ![]() :
:
![]() ;
; ![]() .
.
Показать, что эти векторы ортогональны.
1.2.
Доказать коллинеарность
векторов ![]() и
и ![]() :
:
![]() ;
;
![]() .
.
1.3. Найти скалярное, векторное произведения и угол
между векторами ![]() и
и ![]() :
: ![]() ;
; ![]() .
.
1.4. Найти уравнение силовой линии вектора ![]() .
.
1.5. Построить поле радиус-вектора ![]() .
.
1.6. Построить поле вектора ![]() .
.
1.7. Найти уравнение линии вектора ![]() .
.
1.8. Задан потенциал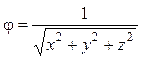 .
.
Найти градиент этого потенциала. Какую форму будyт иметь эквипотенциальные поверхности?
1.9. Даны векторы![]() и
и ![]() :
:
![]() ;
; ![]() .
.
Найти градиент скалярного произведения этих векторов.
1.10. Подсчитать поток радиус-вектора ![]() сквозь полную
поверхность прямого
сквозь полную
поверхность прямого
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.