


1.1 Точные алгоритмы (без ограничения на степени вершин).
1.1.1Алгоритм Краскала
1.1.2Алгоритм использующий пометки вершин
1.1.3Алгоритм Прима
1.2 Алгоритм построения КСД с ограничением на степени вершин
1.2.1 Модифицированный алгоритм Прима
1.2.2 Алгоритм построения дерева-цепочки
2. Алгоритм построения матрицы контуров и сечений
Приведём некоторые сведения из теории графов, необходимые для рассмотрения последующих задач.
Графом G(X,U) называют совокупность двух множеств: Х={x1,x2,...xn} - множество вершин и U={u1,u2,...um}- множество дуг в ориентированном графе (рёбер в неориентированном) вида uk=(xi,xj), xi,xjОX.
Путём в ориентированном графе (маршрутом в неориентированном) называется последовательность дуг (ребер), в которой конечная вершина каждой (кроме последней) дуги (ребра) является начальной вершиной следующей дуги (ребра).
Связным называется граф, в котором для любой пары вершин существует хотя бы один путь (маршрут).
Замкнутым путём (маршрутом) называют путь (маршрут), в котором начальная вершина первой дуги (ребра) и конечная вершина последней дуги (ребра) совпадают.
Если в замкнутом пути (маршруте) каждая его дуга (ребро) встречается не более одного раза, то он называется циклом.
Деревом называется связный неориентированный граф без циклов, или граф, содержащий n вершин и n-1 рёбер.
Ориентированное дерево представляет собой ориентированный граф без циклов, в котором полустепень захода каждой вершины (число дуг, заходящих в вершину), кроме одной, называемой корнем дерева, равна 1, а полустепень захода корня дерева равна 0.
Остовным деревом или остовом графа называют дерево, содержащее все вершины графа.
Заметим, что в неориентированном графе всегда может быть построен остов, в то время как не всякий ориентированный граф содержит остов. Например, ориентированный граф, изображённый на рис.1.1 не содержит остова; если же убрать ориентацию дуг, то можно построить, например, остов, представленный на рис.1.2.
![]()
![]()
![]()
![]()
 |
|||
 |
|||
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Рис.1.1.Орентированный граф . Рис.1.2.Остовное дерево.
Очевидно, что остовов в графе может быть множество; Кэли показал [ ],что если граф с n вершинами полный, то количество остовных деревьев равно nn-2 ,другими словами, на n вершинах можно построить nn-2 остовных деревьев. Будем называть их, деревьями. Произвольное дерево на графе может быть построено, например, методом поиска в глубину.
Дан связный неориентированный граф G(X,U),содержащий n вершин. Обозначим здесь и в последующем через Т множество вершин строящегося графа, через А -множество ребер.
Шаг 1.Выбрать произвольно начальную вершину Xs. Т={Xs};А=0; последняя включенная в дерево вершина p=Xs.
Шаг 2.Если множество F=F(p) Ç(X\T) ¹0,т.е. среди вершин, смежных с p, имеются не вошедшие в поддерево Т, то любую из вершин Хj ÎF включить в дерево: T=TÈXj ;A=A È(pj , xj ).Положить р=хj .Если ïTï=n, то дерево построено, иначе повторить шаг2. Если F=0 ,то вернуться в множество Т к вершине, предшествующей вершине р , принять ее за вершину р и повторить шаг 2.
Если ребрам графа приписаны веса , которые могут иметь различный физический смысл (длина ребра, стоимость, время прохождения сигнала и т.п.),то суммарный вес ребер, вошедших в дерево, называют длиной дерева.
В большинстве прикладных задач требуется найти дерево минимальной длины; будем называть его кратчайшим связывающим деревом - КСД.
1. Алгоритмы построения кратчайших связывающих деревьев.
2. Точные алгоритмы.
3. Алгоритм Краскала.
Дан связный неориентированный граф G(X,U), содержащий n вершин и описываемый взвешенной матрицей сложности.
Шаг 1. Все ребра графа G упорядочить по неубыванию их весов.
Шаг 2. Начав с первого ребра в этом списке ,добавлять следующее ребро, если оно не образует цикла в строящемся дереве.
Шаг 3. Повторять шаг2 до тех пор , пока число ребер в дереве не станет равным n-1.
Приведем пример использования алгоритма Краскала.
Пример 1.1. для графа , представленного на рис.1.3 и заданного матрицей Д , построить КСД.

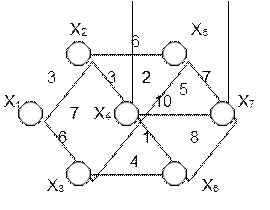 |
![]()
![]() 0 3
6 ì ì ì ì
0 3
6 ì ì ì ì
3 0 7 3 6 ì ì
6 7 0 3 ì 4 ì
Д= ì 3 3 0 2 1 10
ì 6 ì 2 0 5 7
ì ì 4 1 5 0 8
ì ì ì 10 7 8 0
Рис.1.3. Представление графа для примера 1.1.
Список упорядоченных ребер: ( Х4, Х6),(Х4,Х5),(Х1,Х2),(Х2,Х4),(Х3,Х4),(Х3,Х6),
(Х5,Х6),(Х1,Х3),(Х2,Х5),(Х2,Х3),(Х5,Х7),(Х6,Х7),(Х4,Х7).
Дерево с семью вершинами должно содержать пять ребер.
Полученное дерево длиной L=19 изображено на рис.1.4.
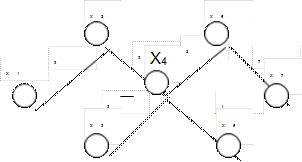 |
![]()
Рис.1.4. КДС для графа на рис.1.3.
Заметим, что ребра (Х3,Х6),(Х5,Х6),(Х1,Х3),(Х2,Х5),(Х2,Х3) не включены в дерево , т.к. они образуют циклы.
В алгоритме Краскала наибольшие затраты времени приходятся на шаг 1, поэтому алгоритм больше подходит для графов с небольшим числом ребер, чем для полных графов. К недостаткам алгоритма можно отнести необходимость проверки на образование цикла при включении в дерево каждого следующего ребра. От этого недостатка свободен алгоритм , использующий пометки вершин , который так же, как и алгоритм Краскала, целесообразно использовать для неполного графа.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.