Число уровней квантования. Допустимая относительная среднеквадратическая погрешность (СКП) восстановления сообщения

Расчет мощности Px отклика ФНЧ произведем по следующей формуле:

2  fa

Px   0

2Ga(f) df  3.3999999999999883968

Px  3.39999999999999

_

Pa  3.4

Среднеквадратическая погрешность фильтрации ф найдем из соотношения:

           ф    Pa  Px                     ф  1.075  10^{ 7}

Учитывая,что   fa= fв получим соотношения для определения частоты fd и интервала T временной дискритизации отлика ФНЧ:

              fd  2fa         fd  6.702  10³

1

              T            T  1.492  10 4

2fa

1.4. Расчет интервала квантования q, порога квантования h(l)и СКП квантования q квантователя АЦП; распределения вероятностей p(l)и интегрального распределения вероятностей F(l);энтропии Hy,производительности Hy1 и избыточности ry квантованной последовательности.

Расчет интервала квантования q произведем по следующей формуле:

                                  6 P_x

                        q                ,где Px-мощность отклика ФНЧ; L -число уровней

                                       L    2

квантования

q  1.844

Пороги квантования можно определить из следующего соотношения:

h(l)  3 Px^ _0.5l_L 1 ₁  1^ l  1 2  7

Уровни квантования определяются следующими соотношениями:

                     l  0 1  7        xo  q          x(l)  xo  l q

                         h(l)                                       x(l) 

-7.376		-6.454
-5.532		-4.61
-3.688		-2.766
-1.844		-0.922
0		0.922
1.844		2.766
3.688		4.61
5.532		6.454

ФПВ гауссовской величины определяется  следующим соотношением:

 x2

2Pa

e

Wx(x) 

2Pa

Постоянная k определяется следующим образом:

0.5L1

k   2q  W_x(x(l))          k  1

l   0

Распределение вероятностей дискретной случайной величины определим используя табулированную функцию Лапласа:

Табулированная функция Лапласа:

              F(x)       x e t2 dt   21  erf 1 x2 122 21  21  1 2 12  21

                                 1                     2                1 2         1

                                 2 _{ }                       2      ¹  2        2                       2              

 2

Распределение вероятностей p(l): p(l)  F h l(  1)  F h(l) 

                                    

p(l) 

1.318·10    -3
0.021
0.136
0.341
0.341
0.136
0.021
1.318·10    -3

Мощность Py квантованного процесса  y[k]  вычислим по формуле:

0.5L1

P_y  2  x(l)²p(l) l  0

Py  3.679

В результате получили выражения для вычисления СКП квантования q квантователя АЦП:

                          q  Px(1  2k)  Py                        q  0.279

Интегральное распределение вероятностей находим по формуле:

l

                               F(l)   p(i)                 F(l) 

1.318·10    -3
0.023
0.159
0.5
0.841
0.977
0.999
1

i  0

Энтропия Hy квантованной последовательности определяется соотношением: L1

Hy   p(l) ln(p(l))ln( )2         Hy  2.104 l  0

Производительность Hy1 или скорость ввода информации в ДКС  определяется соотношением:

        Hy1   T1 Hy Hy1  1.41  104

Для определения избыточности последовательности необходимо определить максимальное значение энтропии.

ln(L)

                 Hmax  ln( )2                Hmax  3

Избыточность последовательности находим из следующего соотношения:

                                        

Hmax  Hy

                     ry       Hmax                  ry  0.299

1.5     Построение таблицы кодовых расстояний  и определение ширины спектра f_икм сигнала ИКМ.

                   ^0  1    1    2    1    2    2  3 ^    n0  1     n1     n2    n3  n4 

                  ^11 02 20  11 22  13 31 22           n5    n6  13   n7  0

                                                 

         ^{ } 21 12 12  03 30  21 21 21  n₀  L1 n_lp(l)       n₁  n₀           n₀  0.5

                   2  1    3    2    1    0    2  1 ^            l  0

                     2   3    1    2    1    2    0   1                       _{0 0}  0

                   3  2    2    1    2    1    1  0 ^

Для определения ширины спектра fикм сигнала ИКМ введем постоянную k1 от 1.5 до 2.

k1  1.75

                                                            ln(L)                                         ⁴

                 fикм  2fak1 ln( )2        fикм  3.519  10

Длительность элементарного кодового символа определяется по формуле:

                                      T                                              ^{ 5}

                      и                    и  4.973  10

1.6 Расчет и построение спектра сигнала дискретной модуляции и определение ширины его спектра fs.

Ширина спектраfs сигнала ДАМ может быть определена так:

                     fs  2fикм                     fs  7.037  10⁴

h       16.5

Определим мощность гауссовского белого шума Pш,

                        P_ш  G_of_s       P_ш  105.56

Мощность сигнала дискретной модуляции,обеспечивающая требуемое отношение сигнал-шум(ОСШ)

                     Ps  Pшh²                Ps  1.742  10³

Средняя мощность и амплитуда на один двоичный символ

Ps

                        Pдам  2         Um    Pдам        Um  29.511

Рассчитаем спектр сигнала ДАМ

                                                                       1                                          ⁴

i   5  3  5           fи  2и fи  1.005  10

Um

S(i) i i  (i)  fo  и

                                l  0         S0(l)  0.5Um              0(l)  fo

Таблицы    значений  S(i)и  ( )i

                               S(i)                                                                   (i) 

1.879		2.701·10  6
3.131		2.66·10  6
9.393		2.62·10  6
9.393		2.58·10  6
3.131		2.54·10  6
1.879		2.499·10  6

Спектр сигнала дискретной амплитудной модуляции

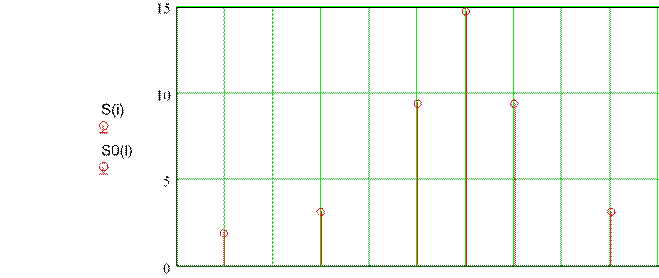
2.48^10⁶2.5^10⁶2.52^10⁶2.54^10⁶2.56^10⁶2.58^10⁶2.6^10⁶2.62^10⁶2.64^10⁶2.66^10⁶2.68^10⁶2.7^10⁶2.72^10⁶ (i)0(l)

1.7       Расчет пропускной способности С гауссовского НКС; построение графиков: ФПВ мгновенных значений гауссовской помехи,ФПВ огибающей узкополосной гауссовской помехи,ФПВ мгновенных значений  Z(t) и огибающей суммы гармонического сигнала и УГП.

Пропускная способность С гауссовского НКС

 log1  h2

     С  fs log( )2                   С  2.906  105

ФПВ мгновенных значений гауссовской помехи

 ²

  50 50

                                                1            2Pш

Wш( ) e

2Pш



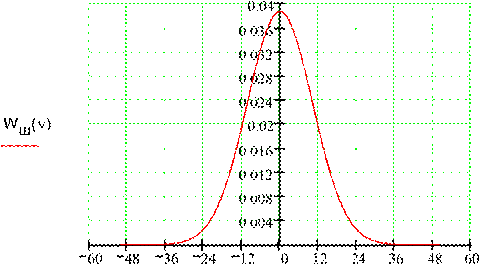
ФПВ огибающей узкополосной гауссовской помехи

-  ²

                                                           2Pш                                 0 0.1  55

Wnm( )  Pш e

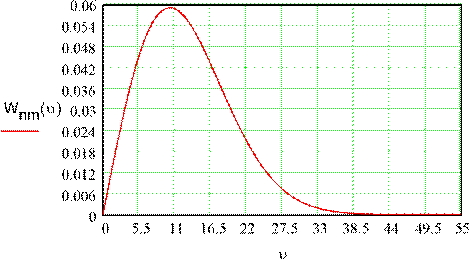
ФПВ мгновенных значений  Z(t)

 Wz( )    

1

 Pш 0

  e

2Pш

  d

 Umcos()2 

  100 99.9 100

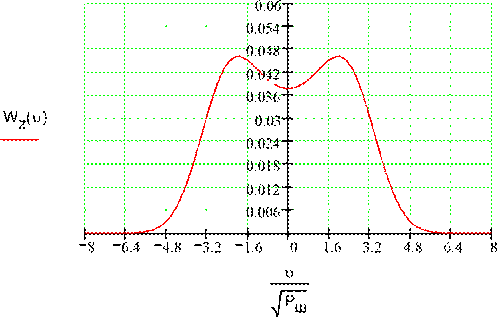
ФПВ огибающей принимаемого сигнала

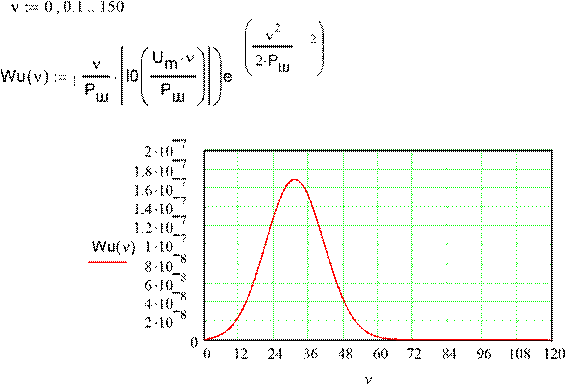-  h





1.8 Расчет средней вероятности ошибки pош и скорости R2  передачи информации по двоичному симметричному ДКС; показателя эффективности Э передачи сигнала дискретной модуляции по НКС.

Для определения средней вероятности ошибки pош воспользуемся табулированной функцией Лапласа:

              F(x)       x e t₂ dt   1  erf 1 x2 122 21  21  1 2 21  21

                                 1                     2                1 2 2       1

                                 2 _{ }                       2      1  2        2                       2              

 2

Средняя вероятность ошибки

                   p_ош  1  ^F h   ^p_ош  2.038  10^{ 3}



Скорость передачи информации по двоичному симметричному ДКС определим из следующего выражения:

1      ln p

R2   и1  pош ln ( )ош2   1  pош ln1ln( )2pош                                              R2  1.968  104



Эффективность Э передачи сигнала дискретной модуляции по НКС:

Э  R²        ,где С  2.906  10⁵ - пропускная способность гауссовского НКС С

Э  0.068

1.9 Расчет скорости передачи информации   Rl по L-ичному ДКС и относительных потерь в скорости передачи информации; СКП шума передачи     п и относительную суммарную СКП  восстановления непрерывного сообщения.

                i  0 1  7        j  0 1  7 Pemi j  p_ош^{i j} 1  pош^{3i j}

Распределение вероятностей принятых L-ичных уровней