Алгоритм построения дерева-цепочки. Ребро максимальной длины в маршруте. Алгоритм построения матрицы контуров и сечений, страница 2

         ребро  (x₃,x₁):  DL(x₅)=7+8-4=11;

DL(x₆)=9+7-4=12;

         ребро  (x₁,x₄):  DL(x₅)=6+3-2=7;

DL(x₆)=7+4-2=9;

         ребро  (x₄,x₂):  DL(x₅)=3+8-1=10;

DL(x₆)=4+6-1=9;

     min    min  DL=7;  x_r=x₅;  (x_i*,x_j*)=(x₁,x₄);

(x,x)ÎM   x_rÎx\T                        

T={x₁,x₂,x₃,x₄,x₅};  M={(x₂,x₃),(x₃,x₁),(x₁,x₅),(x₅,x₄),(x₄,x₂)};  x\T={x₆}.

  Итер 4.  Удалить  можно  ребро  маршрута  (x₂,x₃) или (x₃,x₁) или (x₁,x₅)

               или (x₅,x₄) или (x₄,x₂):

          ребро  (x₂,x₃):  DL(x₆)=6+9-3=12;

          ребро  (x₃,x₁):  DL(x₆)=9+7-4=12;

           ребро  (x₁,x₅):  DL(x₆)=7+8-6=9;

           ребро  (x₅,x₄):  DL(x₆)=8+4-3=9;

           ребро  (x₄,x₂): DL(x₆)=4+6-1=9;

            min    min  DL=9;   x_r=x₆;  (x_i*,x_j*)=(x₁,x₅)-выберем  первое  среди 

(x_i,x_j)ÎM  x_rÎx\T                                                  эквивалентных

   Маршрут  M={(x₂,x₃),(x₃,x₁),(x₁,x₆),(x₆,x₅),(x₅,x₄),(x₄,x₂)}.

Шаг 3.  Ребро  максимальной  длины  в  маршруте  d(x₆,x₅)=8.

              Удалив  его  из  маршрута , получим  дерево-цепочку :

x₅-x₄-x₂-x₃-x₁-x₆  длиной  L=18,  представленное  на  рис.1.6.

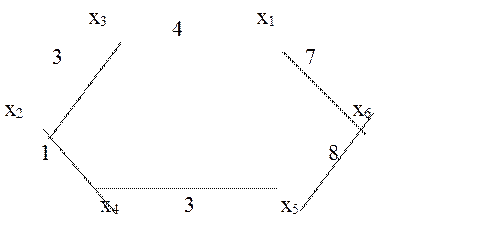                                                           Рис.1.6.

2.Агоритм   построения  матрицы  контуров  и  сечений .

Матрица  контуров  и  сечений  (M - матрица )  для  ориентированного  графа 

формируется  следующим  образом . На  графе  строится  основное  дерево  (будем  рассматривать  графы , для   которых  основное  дерево  существует) .

Дуги  образующие  дерево , называют  ветвями , дуги , не  вышедшие  в  дерево - хордами.

Число  строк  в  M - матрице  соответствует  числу  хорд , а  число  столбцов    соответствует  числу  ветвей  .

Каждая  хорда  графа  поочередно  включается  в  дерево , при  этом  образуется  цикл  (контур).  Выполняется  обход  контура  в  направлении , заданном  направлении  хорды ; в  строке  матрицы , соответствующей  данной  хорде , ставится  +1  для  ветви  дерева , если  ее  направление  совпадает  с  направлением  обхода  контура ; -1 , если  направление  противоположно ; 0 , если  ветвь  не  входит  в  данный  контур.

Пример 2.1:  дан  ориентированный  граф  G(x , u) , содержащий  6  вершин  и    

                       12  дуг .

Методом  поиска  в  глубину , начиная  с  вершины  x₁ ,  строим  дерево.    Дуги , вошедшие  в  дерево , обозначим  буквами , хорды  пронумеруем .     

M - матрица  имеет  5  столбцов  и  7  строк .  

	а	б	в	г	д
1	-1	0	-1	0	0
2	-1	0	-1	-1	0
3	0	-1	1	0	0
4	0	0	1	1	0
5	1	0	1	0	1
6	0	-1	1	0	1
7	0	0	0	-1	1

         Рис.2.1.     

                                       М - матрица  для  графа  на  рис.2.1.   

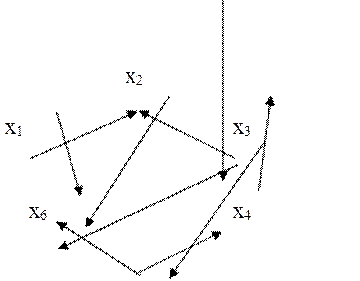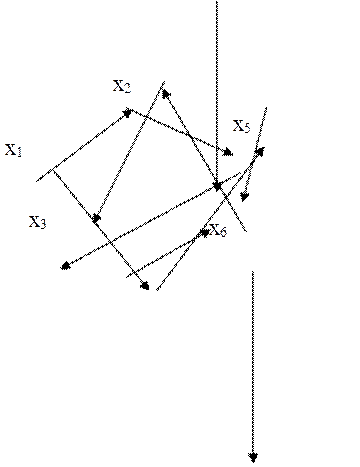                   Рис.2.2.                                                                Рис.2.3

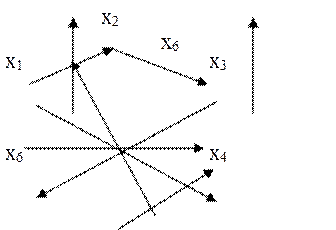                    Рис.2.4.                                                                 Рис.2.5.

                                                          Рис.2.6.

                             Начинать  с  вершины  x₁.