this routine on an AT90Sxx0x, add an “INC ZL” instruction where indicated in the file listing.
“bin2BCD16” implements the following algorithm:
1. Load loop counter with 16.
2. Clear all three bytes of result.
3. Shift left input value low byte.
4. Shift left carry into input value high byte.
5. Shift left carry into result byte 0 (two least significant digits).
6. Shift left carry into result byte 1.
7. Shift left carry into result byte 2 (most significant digit).
8. Decrement loop counter
9. If loop counter is zero, return from subroutine.
10. Add $03 to result byte 2.
11. If bit 3 is zero after addition, restoreold value of byte 2.
12. Add $30 to result byte 2.
13. If bit 7 is zero after addition, restoreold value of byte 2.
14. Add $03 to result byte 1.
15. If bit 3 is zero after addition, restoreold value of byte 1.
16. Add $30 to result byte 1.
17. If bit 7 is zero after addition, restoreold value of byte 1.
18. Add $03 to result byte 0.
19. If bit 3 is zero after addition, restoreold value of byte 0.
20. Add $30 to result byte 0.
21. If bit 7 is zero after addition, restoreold value of byte 0.
22. Goto Step 3. all three bytes of the result. This is shown in the flow chart
In the implementation. Steps 10-21 are carried out inside a below. loop, where the Z-pointer is used for successive access of
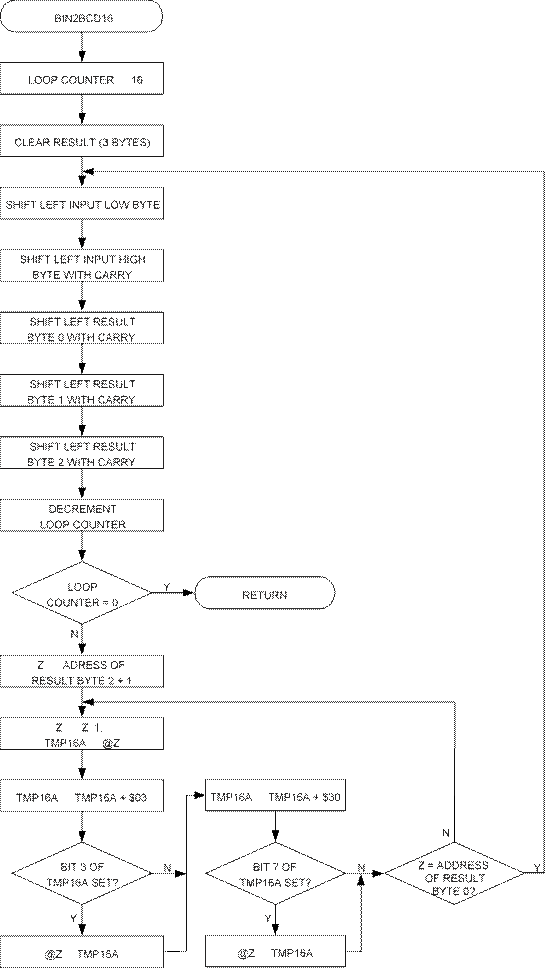
Figure 1. “bin2BCD16” Flow Chart
1. Load the 16-bit register variable “fbinH:fbinL” with the 3. The result is found in the 3-byte register variable
16-bit number to be converted. (High byte in “fbinH”) “fBCD2:fBCD1:fBCD0” with MSD in the lower nibble of
2. Call “bin2BCD16”. “fBCD2”.
Table 2. “bin2BCD16” Register Usage
|
Register |
Input |
Internal |
Output |
|
R13 |
“fBCD0” - BCD digits 1 and 0 |
||
|
R14 |
“fBCD1” - BCD digits 2 and 3 |
||
|
R15 |
“fBCD2” - BCD digit 4 |
||
|
R16 |
“fbinL” - binary value low byte |
||
|
R17 |
“fbinH” - binary value high byte |
||
|
R18 |
“cnt16a” - loop counter |
||
|
R19 |
“tmp16a” - temporary storage |
||
|
R30 |
ZL |
||
|
R31 |
ZH |
Table 3. “bin2BCD16” Performance Figures
|
Parameter |
Value |
|
|
Code Size (Words) |
25 |
|
|
Average Execution Time (Cycles) |
760 |
|
|
Register Usage |
• Low registers • High registers • Pointers |
:3 :4 :Z |
|
Interrupts Usage |
None |
|
|
Peripherals Usage |
None |
This subroutine converts an 8-Bit binary value to a 2-digit BCD number. The implementation does not generate a packed result, i.e. the two digits are represented in two separate bytes. To accomplish this, some smaller modifications must be done to the algorithm as shown in the following section.
“bin2BCD8” implements the following algorithm:
1. Clear result MSD.
2. Subtract 10 from the 8-bit input number.
3. If result negative, add back 10 to 8-bit input number and return
4. Increment result MSD and goto step 2.
LSD of the result is found in the same register as the input number. If a packed result is needed, make the following changes to the algorithm:
• Instead of incrementing MSD in Step 4, add $10 to MSD.
• After adding back 10 to the input number in step 3, addLSD and MSD together.
Where to make these changes is indicated in the program listing.
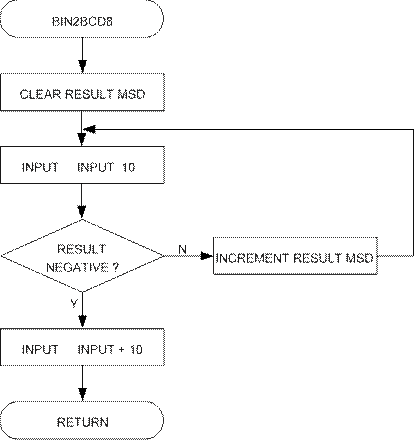
Figure 2. “bin2BCD8” Flow Chart
1. Load the register variable “fbin” with the value to be 3. The result MSD and LSD is found in “fBCDH” and converted. “fBCDL”, respectively.
2. Call “bin2BCD8”.
Table 4. “bin2BCD8” Register Usage
|
Register |
Input |
Internal |
Output |
|
R16 |
“fbin” - binary value |
“tBCDL” - LSD of result |
|
|
R17 |
“tBCDH” - MSD of result |
Table 5. “bin2BCD8” Performance Figures
|
Parameter |
Value |
|
|
Code Size (Words) |
6 + return |
|
|
Average Execution Time (Cycles) |
28 |
|
|
Register Usage |
• Low registers • High registers • Pointers |
:None :2 :None |
|
Interrupts Usage |
None |
|
|
Peripherals Usage |
None |
This subroutine converts a 5-digit packed BCD number to a 16-Bit binary value.
Let a, b, c, d, e denote the 5 digits in the BCD number (a = MSD, e = LSD). The result is generated by computing the following equation:
10 10 10 10( ( ( a b+ ) +c) +d) +e
The four times repeated operation “multiply-by-10-and-add” is implemented as a subroutine. This subroutine takes the 16-bit register variable “mp10H:mp10L” and the register variable “adder” as input parameters. The subroutine can be called by two separate addresses, “mul10a” and “mul10b”. The difference is summarized as follows:
“mul10a” - multiplies “mp10H:mp10L” and adds the higher nibble of “adder”.
“mul10b” - multiplies “mp10H:mp10L” and adds the lower nibble of “adder”.
The subroutine implements the following algorithm.
1. Swap high/low nibble of “adder”
2. Make a copy of “mp10H:mp10L”.
3. Multiply original by 2 (Shift left).
4. Multiply copy by 8 (Shift left x 3).
|
Register |
Input |
Internal |
Output |
|
R12 |
“copyL” - temporary value used by “mul10a/mul10b” |
||
|
R13 |
“copyH” - temporary value used by “mul10a/mul10B” |
||
|
R14 |
“mp10L” - low byte of input to be multiplied by “mul10a/mul10b” |
“tbinL” - low byte of 16-bit result |
|
|
R15 |
“mp10H” - high byte of input to be multiplied by “mul10a/mul10b” |
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.