Лабораторная работа № 1
Изучение методов дискретизации и квантования сигналов, ознакомление с правилами выбора основных параметров устройств дискретизации и квантования, оценка возникающих погрешностей и их качественный визуальный контроль.
1.1.1. Принцип дискретизации по времени заключается в том, что непрерывный сигнал x ta ( ) заменяется последовательностью его мгновенных значений x t( k ) (отсчетов) (рис.1), взятых в определенные дискретные моменты времени tk = k tΔ , где k = 0, 1, 2, …, и разделенных промежутками времени Δt .
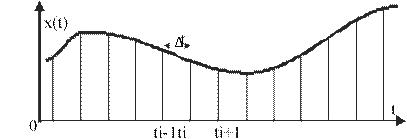
Рис. 1. Аналоговый сигнал и последовательность его отсчетов
При такой замене из рассмотрения исключается всё множество значений x ta ( ), находящихся внутри интервала Δt . Если Δt - const, то дискретизация называется равномерной с периодом τп =Δt . В общем случае положение отсчетов может быть неравномерным. Например, они могут сгущаться и разряжаться в соответствии со скоростью изменения сигнала. Это адаптивная дискретизация. Наибольшее распространение получила равномерная дискретизация из-за простоты технической реализации.
В основе математического описания дискретизации непрерывных функций лежит так называемая импульсная функция дискретизации
aД(
)t
(t k t),
где δ(t − k tΔ )
- дельта-функция.
k=−∞
Дискретизация непрерывной функции времени x t( ) с математической точки зрения представляет собой умножение x t( ) на aД(t):
∞
xД( )t = x t a( ) Д( )t = ∑ x ta( ) (δ t − Δk t).
k=−∞
Используя фильтрующее свойство δ - функции
, можно записать x ta ( )δ(t − k tΔ )=
x k ta (
Δ
)
(δ
t −
k tΔ
).
То есть умножение x t(
) на единичный δ -импульс соответствует получению
отсчета функции x t(
) в момент времени tk
= k tΔ .
Тогда окончательно для дискретной функции имеем:
∞
xД( )t = ∑x k ta( Δ δ − Δ) (t k t).
k=−∞
На практике дискретизация реализуется с помощью ключевых схем.
При дискретизации по времени возникают задачи, связанные с выбором интервала Δt и восстановлением исходного сигнала на выходе по его отсчетам. Решение этих задач зависит от вида дискретизируемого сигнала.
Сложность задачи выбора интервала дискретизации состоит в том, что необходимо учитывать свойства обрабатываемых сигналов, способ восстановления этих сигналов по отсчетам, требуемую точность восстановления.
● Непрерывные реальные сигналы являются, как правило, нестационарными случайными процессами, которые характеризуются всей совокупностью возможных реализаций. Однако часто возможно считать такой сигнал стационарным или кусочно-стационарным. Кроме того, часто полагают сигнал еще и эргодическим, что дает возможность работать не с ансамблем реализаций случайного сигнала, а только с одной его реализацией. При условии TcΔFэ >>1 (Tc - длительность интервала обработки сигнала; ΔFэ - ширина его спектра) погрешностями из-за такого предположения можно пренебречь.
● 
Сигнал обычно характеризуют
либо энергетическим спектром, либо его корреляционной функцией. Энергетический спектр
G(
)ω
может быть выражен через спектр сигнала S j( ω).
Если амплитудный спектр одной из реализаций сигнала x ta ( ) равен
S j(
ω),
то энергетический спектр S(ω
=)
lim m S j{
(
ω)2
/ Tc},
Tc→∞
где m - символ математического ожидания.
● На дискретизируемый процесс часто накладывают ограничения:
− конечное значение средней мощности процесса
1 Tc
Px = 
∫x t dt
< ∞ ;
Tc 0
− конечная шкала мгновенных
значений max x t(
) ≤
xm ;
− ограничение спектра по полосе. Спектральная плотность любого реального сигнала уменьшается с ростом частоты. Начиная с некоторой частоты, спектральная плотность сигнала становится меньше спектральной плотности помех и шумов. Эта часть спектральной плотности сигнала почти не вносит вклада в полезную информацию и ею можно пренебречь. Ограничение спектра сообщения частотой ωB приводит к ошибке
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.
