Оценка степени дифференциации доходов населения. Методы оценки степени дифференциации доходов населения

Проверка гипотезы о предполагаемом законе распределения (т.е. о том, что совокупность действительно распределена по логнормальному закону) производится при помощи специально подобранной величины - критерия согласия.

Критерием согласия называют критерий проверки гипотезы о предполагаемом законе неизвестного распределения.

Имеется несколько критериев согласия: (”хи квадрат”) К. Пирсона, Колмогорова, Смирнова и др. Ограничимся описанием применения критерия Пирсона к проверке гипотезы о логнормальном распределении генеральной совокупности. С этой целью сравниваются эмпирические  (наблюдаемые) и теоретические (вычисленные в предположении логнормального распределения) частоты. Обычно эмпирические и теоретические частоты различаются. Случайно ли это расхождение? Критерий Пирсона отвечает на этот вопрос. Правда, как и любой критерий, он не доказывает справедливость гипотезы, а лишь устанавливает на принятом уровне значимости ее согласие или несогласие с данными наблюдений.

Уровнем значимости называют вероятность того, что будет отвергнута правильная гипотеза. Уровень значимости обозначают обычно . Наиболее часто уровень значимости принимают равным 0.05 или 0.01. Если, например, принят уровень значимости, равный 0.05, то это значит, что в пяти случаях из 100 имеется риск отвергнуть правильную гипотезу, т.е. отвергнуть гипотезу о логнормальном распределении элементов совокупности.       

В качестве критерия проверки гипотезы принимают случайную величину

,        (5)

где n_i - эмпирические частоты;

n_i^/ - теоретические частоты.

Эта величина случайная, так как  в различных опытах она принимает различные, заранее неизвестные значения. Ясно, что чем меньше различаются эмпирические и теоретические частоты, тем меньше величина критерия и поэтому этот критерий характеризует близость эмпирического и теоретического распределений.  Теоретические частоты находятся с помощью формулы (1).

Итак, для того чтобы при заданном уровне значимости проверить гипотезу о логнормальном распределении совокупности, нужно вычислить наблюдаемое значение критерия

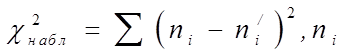         (6)

и по таблице критических точек распределения , заданному уровню значимости   и числу степеней свободы k = s-3 (s - число интервалов выборки) найти критическую точку  (; k).

Если  _набл  < _кр  гипотеза верна.

Если  _набл  > _кр - гипотеза отвергается.

Расчет коэффициента Джини производится на основании данных о распределении населения по уровню среднедушевого совокупного дохода. Вся совокупность получателей доходов делится на 5 равных групп (определяется, какой долей дохода владеет каждая группа населения. Затем по полученным накопленным итогам строится так называемая кривая Лоренца (графическое изображение уровня концентрации явления).

Ряд распределения делится на квинтельные группы в зависимости от уровня среднедушевого дохода (по 20 % населения в каждой начиная от низкодоходных групп к высокодоходным).

Квантиль - это значение х_q случайной величины, удовлетворяющей условию:

                    F(x_q) = q,               (7)

где F(x_q)- вероятность того, что Х<x.

Различают

медиану  при q=0.5

квартели при q=0.25

квинтели при q=0.2

децили при q=0.1

процентили при q=0.01

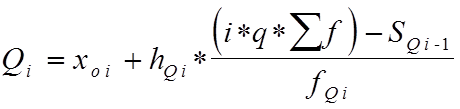  ,  (8)

где i- номер квантиля;

x_0i - нижняя граница квантильного интервала;

h_Qi - величина соответствующего интервала;

S_{Qi - 1} - накопленные частоты предшествующих интервалов;

f_{Q i} - частоты квантильного интервала;

f -  сумма всех частот.

В каждой группе определяется средний доход, приходящийся на душу населения. Перемножая средние доходы на 1/5 общей численности населения, находим, каким доходом владеет каждая группа населения. Затем, определив суммарные доходы общества, рассчитываем их процентное распределение по квинтелям населения.

Для построения кривой Лоренца на осях координат с процентной шкалой от 0 до 100 откладываются кумулятивные (накопленные) итоги распределения доходов по типу "менее чем": на горизонтальной оси - квинтели получателей доходов, на вертикальной - проценты полученных доходов. Кривая Лоренца получается путем соединения точек, соответствующих кумулятивным процентным долям доходов, полученных квинтельными группами населения.

Схематично график выглядит следующим образом:

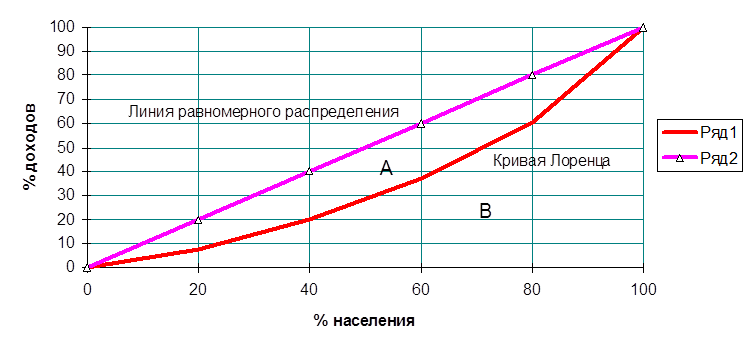
При равномерном распределении доходов каждая двадцатипроцентная группа населения имела бы пятую часть доходов общества. На графике это изображается диагональю квадрата и рассматривается как линия равномерного распределения. При неравномерном распределении "линия концентрации" представляет собой вогнутую вниз кривую.  Чем больше отклонение кривой Лоренца от диагонали квадрата, тем выше поляризация доходов общества.

Определим вид функции, которой можно описать кривую Лоренца