Speed is Comparable with HW mance specifications is given in Table 1.
Multiplicators/Dividers
Example: 8 x 8 Mul in 2.8 ms, 16 x 16
Mul in 8.7 µs (12 MHz)
• Extremely Compact Code
Table 1. Performance Figures Summary
|
Application |
Code Size (Words) |
Execution Time (Cycles) |
|
8 x 8 = 16 bit unsigned (Code Optimized) |
9 |
58 |
|
8 x 8 = 16 bit unsigned (Speed Optimized) |
34 |
34 |
|
8 x 8 = 16 bit signed (Code Optimized) |
10 |
73 |
|
16 x 16 = 32 bit unsigned (Code Optimized) |
14 |
153 |
|
16 x 16 = 32 bit unsigned (Speed Optimized) |
105 |
105 |
|
16 x 16 = 32 bit signed (Code Optimized) |
16 |
218 |
|
8 / 8 = 8 + 8 bit unsigned (Code Optimized) |
14 |
97 |
|
8 / 8 = 8 + 8 bit unsigned (Speed Optimized) |
66 |
58 |
|
8 / 8 = 8 + 8 bit signed (Code Optimized) |
22 |
103 |
|
16 / 16 = 16 + 16 bit unsigned (Code Optimized) |
19 |
243 |
|
16 / 16 = 16 + 16 bit unsigned (Speed Optimized) |
196 |
173 |
|
16 / 16 = 16 + 16 bit signed (Code Optimized) |
39 |
255 |
The application note listing consists of two files:
“avr200.asm”: Code size optimized multiplied and divide routines.
“avr200b.asm”: Speed optimized multiply and divide routines.
 |
The algorithm for the Code Size optimized version is as follows:
1. Clear result High byte.
2. Load loop counter with 8.
3. Shift right multiplier
4. If carry (previous bit 0 of multiplier) set, add multiplicand to result High byte.
5. Shift right result High byte into result Low byte/multiplier.
6. Shift right result Low byte/multiplier.
7. Decrement Loop counter.
|
Figure 1. “mpy8u” Flow Chart (Code Size Optimized Implementation)
|
8.
If loop counter not zero, goto Step 4.
The usage of “mpy8u” is the same for both versions:
1. Load register variables “mp8u” and “mc8u” with the multiplier and multiplicand, respectively.
2. Call “mpy8u” Performance
3. The 16 -bit result is found in the two register variables “m8uH” (High byte) and “m8uL” (Low byte)
Observe that to minimize register usage, code and execution time, the multiplier and result Low byte share the same register.
Table 2. “mpy8u” Register Usage (Code Size Optimized Implementation)
|
Register |
Input |
Internal |
Output |
|
R16 |
“mc8u” - multiplicand |
||
|
R17 |
“mp8u” - multiplier |
“m8uL” - result Low byte |
|
|
R18 |
“m8uH” - result High byte |
||
|
R19 |
“mcnt8u” - loop counter |
Table 3. “mpy8u” Performance Figures (Code Size Optimized Implementation)
|
Parameter |
Value |
|
|
Code Size (Words) |
9 + return |
|
|
Execution Time (Cycles) |
58 + return |
|
|
Register Usage |
• Low registers • High registers • Pointers |
:None :4 :None |
|
Interrupts Usage |
None |
|
|
Peripherals Usage |
None |
Table 4. “mpy8u” Register Usage (Straight-line Implementation)
|
Register |
Input |
Internal |
Output |
|
R16 |
“mc8u” - multiplicand |
||
|
R17 |
“mp8u” - multiplier |
“m8uL” - result Low byte |
|
|
R18 |
“m8uH” - result High byte |
Table 5. “mpy8u” Performance Figures (Straight-Line Implementation)
|
Parameter |
Value |
|
|
Code Size (Words) |
34 + return |
|
|
Execution Time (Cycles) |
34 + return |
|
|
Register Usage |
• Low registers • High registers • Pointers |
:None :3 :None |
|
Interrupts Usage |
None |
|
|
Peripherals Usage |
None |
This subroutine, which is found in “avr200.asm” implements signed 8 x 8 multiplication. Negative numbers are represented as 2’s complement numbers. The application is an implementation of Booth's algorithm. The algorithm provides both small and fast code. However, it has one limitation that the user should bear in mind; If all 16 bits of the result is needed, the algorithm fails when used with the most negative number (-128) as the multiplicand.
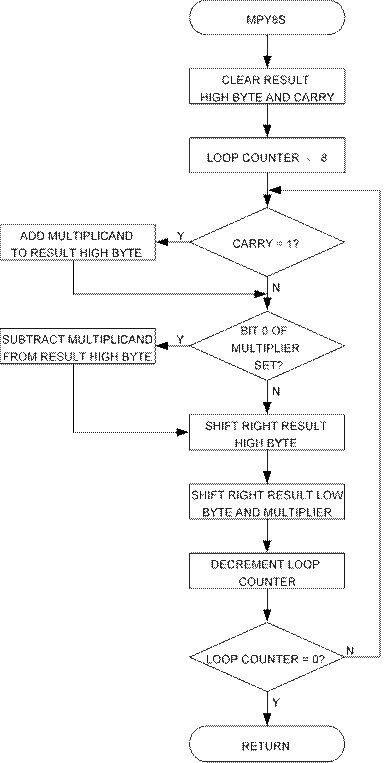
The algorithm for signed 8 x 8 multiplication is as follows:
1. Clear result High byte and carry.
2. Load loop counter with 8.
3. If carry (previous bit 0 of multiplier) set, add multiplicand to result High byte.
4. If current bit 0 of multiplier set, subtract multiplicand from result High byte.
5. Shift right result High byte into result Low byte/multiplier.
6. Shift right result Low byte/multiplier.
7. Decrement loop counter.
8. If loop counter not zero, goto Step 3.
Figure 2. “mpy8s” Flow Chart
The usage of “mpy8s” is as follows: 3. The 16 -bit result is found in the two register vari1. Load register variables “mp8s” and “mc8s” with the ables “m8sH” (High byte) and “m8sL” (Low byte) multiplier and multiplicand, respectively. Observe that to minimize register usage, code and execu2. Call “mpy8s” tion time, the multiplier and result Low byte share the same register.
Table 6. “mpy8s” Register Usage
|
Register |
Input |
Internal |
Output |
|
R16 |
“mc8s” - multiplicand |
||
|
R17 |
“mp8s” - multiplier |
“m8sL” - result Low byte |
|
|
R18 |
“m8sH” - result High byte |
||
|
R19 |
“mcnt8s” - loop counter |
Table 7. “mpy8s” Performance Figures
|
Parameter |
Value |
|
|
Code Size (Words) |
10 + return |
|
|
Execution Time (Cycles) |
73 + return |
|
|
Register Usage |
• Low registers • High registers • Pointers |
:None :4 :None |
|
Interrupts Usage |
None |
|
|
Peripherals Usage |
None |
Both program files contain a routine called “mpy16u” which performs unsigned 16-bit multiplication. Both implementations are based on the same algorithm. The code size optimized implementation, however, uses looped code, whereas the speed optimized code is a straight-line code implementation. Figure 3 shows the flow chart for the Code Size optimized (looped) version.
The algorithm for the Code Size optimized version is as follows:
1. Clear result high word (Bytes 2 and 3)
2. Load loop counter with 16.
3. Shift multiplier right
4. If carry (previous bit 0 of multiplier Low byte) set, add multiplicand to result High word.
5. Shift right result High word into result Low word/multiplier.
6. Shift right Low word/multiplier.
7. Decrement Loop counter.
8. 8. If loop counter not zero, goto Step 4.
|
Figure 3. “mpy16u” Flow Chart (Code Size Optimized Implementation)
|
The usage of “mpy16u” is the same for both versions:
1. Load register variables “mp16uL”/”mp16uH” with multiplier
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.