Основні принципи побудови та використання діодних схем. Малопотужні випрямлячі. Робота випрямляча на активно-реактивне навантаження, страница 3

Тому струм, збуджуємий напругою u₂(t), в інтервалі p/2 ¸  p  протікати не може. З моменту p напруга u₂(t)  зростає з іншою полярністю, внаслідок чого з’являється коло для протікання струму – w₂, VD₃, C_d//R_d, VD₄, w₂ . Але до моменту t₁ миттєве значення u₂(t)   буде меншим, ніж напруга на конденсаторі С_d – u_C , VD₃  буде зміщеним в звортньому напрямку  і струм протікати не буде. Тільки з моменту  t₁, коли u₂(t)  > u_C , появиться струм  в колі, який буде підзаряжати конденсатор в інтервалі часу y.  В результаті такої роботи випрямляча  напруга на навантаженні U_d  і змінна складова  DU_d будуть визначатись  постійною часу R_dC_d   розряду конденсатора на навантаження.

Для визначення розрахункових параметрів виходимо з того, що величина пульсацій напруги DU_d реально не повинна перевищувати 2-5% від U_d . Тому з вказаною похибкою можна стверджувати, що

U_d =Ö2*U₂.

Струм I_d = U_d /R_d , а через послідовно з’єднані діоди випрямляча

I_VD =I_d/2.

Максимальна величина зворотньої напруги, що прикладається до діода  

U_ЗВ.МАХ =Ö2*U₂.

Для знаходження ємкості конденсатора скористаємось лінійною апроксимацією  процесів заряду і розряду конденсаторів. Внаслідок таких спрощень одержана приблизна формула:

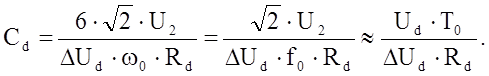
Звернемо увагу на одну особливість роботи випрямляча на активно- ємкісне навантаження. Вона полягає в тому , що споживаємий від мережі струм  представляє собою різнополярну періодичність вузьких імпульсів значної амплітуди, зміщених вліво від середини напівперіода напруги живлення. Звідси витікає, що розглядаємий випрямляч по відношенню до мережі живлення  представляє собою нелінійне навантаження імпульсного характеру з невеликою ємкісною реакцією. В таких ситуаціях, якщо не приймати спеціальних мір , випрямляч може впливати на  інші споживачі мережі, спотворюючи їх роботу. Тому між мережею живлення і споживачем  необхідно встановлювати спеціальний фільтр, який повинен захищати мережу від проникнення в неї перешкод від розглядаємого випрямляча.

Розглянута схема випрямляча при роботі на ємкісне навантаження знаходить дуже широке використання для живлення побутової радіоапаратури, персоналдьних компютерів та інших малопотужних споживачів.

Зовнішні характеристики випрямлячів.

Зовнішньою характеристикою  називається  залежність  величини випрямленої напруги від струму навантаження I_d  і визначається відомою формулою:

U_dн = U_d -I_dR_В, де  R_В – сумарне значення внутрішнього опору випрямляча, яке включає в себе опори обмоток трансформатора, випрямляючих діодів, з’єднуючих провідників.

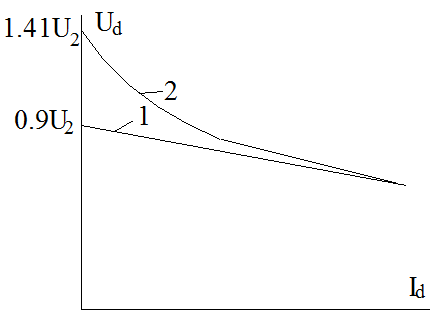На рис.2.5 приведені  зображення зовнішніх характеристик при роботі на акривне ( активно-індуктивне) навантаження ( лінія 1), а також на активно-ємкісне (лінія 2). В режимі холостого ходу напруга має максимальне значення, яке визначається формулами (2.2  ) і (2.5) . При наявності струму навантаження  має місце падіння напруги на внутрішніх опорах, внаслідок чого напруга на

Рис.2.5.                       виході зменшується на величину I_dR_В. Для лінії 2 допоміжно має місце зниження середнього значення напруги завдяки зменшенню величини опрору  R_d  і відповідно,  постійної часу  розряду конденсатора. Тому з ростом струму I_d характеристика має більш крутий нахил і при великих струмах наближається до прямої 1.

Випрямлячі з домноженням напруги.

Подібні схеми  використовуються в тих випадках, коли з''являється необхідність живлення високоомних навантажень високою напругою. Здебільшого вони находять використання для живлення електронно-променевих трубок та кінескопів. Використання подібних схем дає можливість одержати на виході напругу в декілька разів перевищуючу напругу мережі. Як приклад на рис. приведена проста схема, яка забезпечує подвоєння вхідної напруги. Робота її полягає в слідуючому. На вхідні клеми 1-2 підводиться змінна напруга з діючим значенням U₂. При позитивній напівхвилі на клемі 2  відбувається заряд конденсатора С₁ через діод VD₁ до амплітудного значення вхідної напруги U_C=Ö2*U₂. При другому напівперіоді 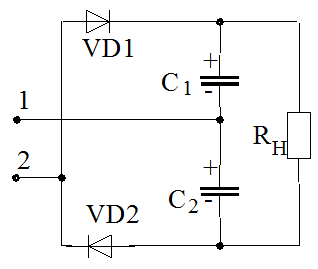вхідної напруги  подібним шляхом відбувається заряд конденсатора С₂. В результаті напруга, що прикладається до навантаження буде визначатись сумою напруг конденсаторів, тобто маємо: