Метод наименьших квадратов. Линейная функция. Эмпирическая линия регрессии. Оценка погрешности прогноза

Требуется спрогнозировать спрос на выпускаемую продукцию на 3 месяца следующего периода.

                  1.Метод наименьших квадратов.

                         1.1.Линейная функция.

Нанесем эмпирическую линию регрессии.

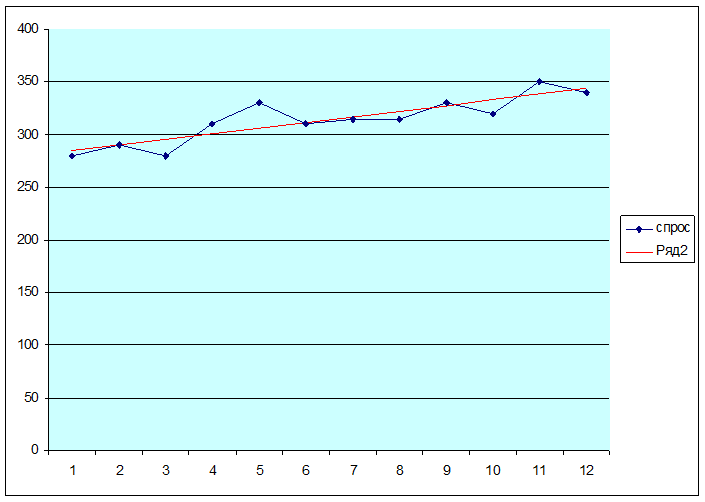
Рис 1. Эмпирическая линия регрессии

Линейная функция имеет вид:

y=at+b

Из теории линейной регрессии известно, что параметры a и b для сглаживающей прямой есть:

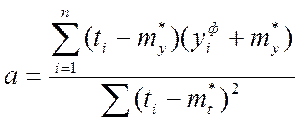
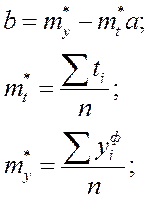
Где y- фактическое значение спроса;

t- номер периода наблюдения.

Определив по формулам значения параметров a и b, получаем зависимость:

m_t=6.5

m_y=314.166

a=5.385;

b=279.166

Получаем уравнение y=5.385t+279.166

                        Оценка погрешности прогноза

Определяем стандартное отклонение

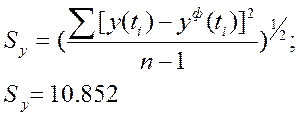
Где y(t) – расчетное значение спроса

y^ф(t) – фактическое значение спроса

Вывод:

Принимая условие, что ошибка прогнозирования подчиняется нормальному закону распределения, можно считать, что с вероятностью, близкой к 1 (0,98), фактический спрос в каждой точке будет находиться в интервале “+” “-“ 32  по правилу 3σ, а с вероятностью 0,95 – в диапазоне “+” ”-” 21 – по правилу 2σ

2.Метод экспоненциального сглаживания.

В этом методе ставится акцент на более поздние наблюдения. Прогнозируемые оценки определяются по формуе:

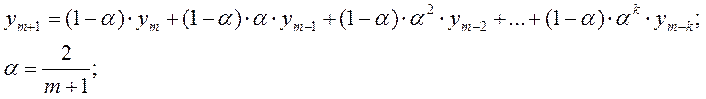
Где α – коэффициент сглаживания

m – число наблюдений у – спрос

Получаем α=0,154

Чем позднее наблюдение, тем больше вес оно имеет.

Высчитываем прогнозируемые значения:

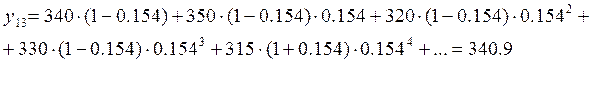
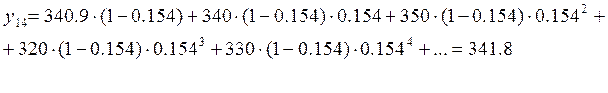
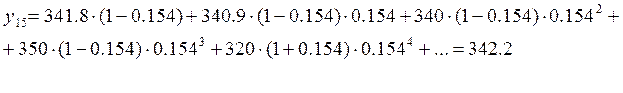
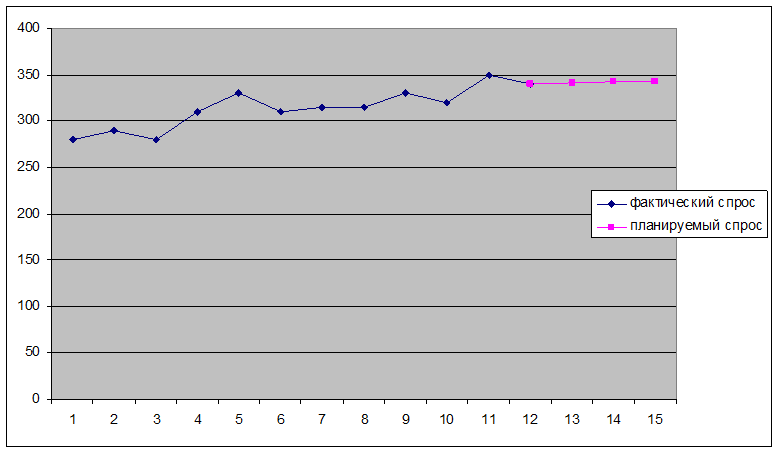
График прогноза по методу экспоненциального сглаживания

Вывод:

Прогноз можно сделать только на один месяц, каждый последующий прогноз можно осуществлять при наличии фактических значений, т.е. дожидаться получения данных.

3.Метод скользящей средней.

Прогнозирование оценки определяется путем расчета среднего арифметического нескольких последних значений. Определим у_m на 3 месяца методом скользящего среднего, беря в расчет среднее арифметическое пяти последних значений.

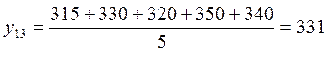
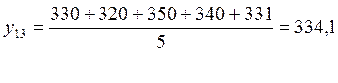
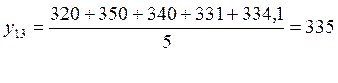
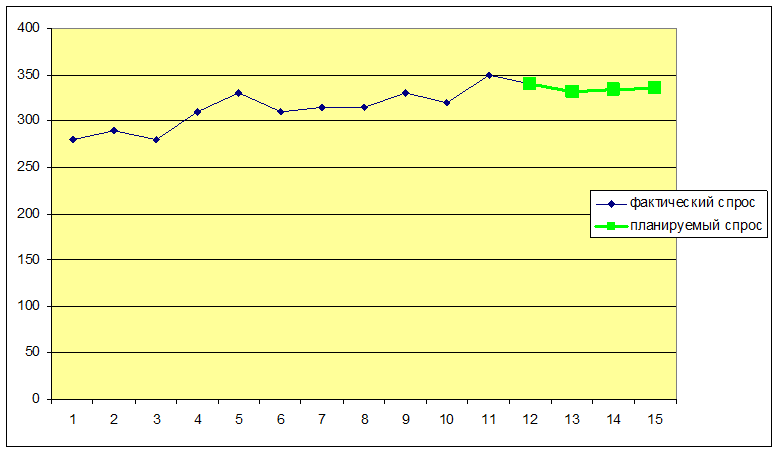
Вывод:

Метод не дает точности прогнозирования на длительный срок, поскольку последующее прогнозируемое значение завысит от предыдущего. Значение можно определить только на один месяц.