Изучение теоретических и практических приёмов нахождения экстремума функций численными методами

Лабораторная работа №2

Цель работы: Изучение  теоретических и практических приёмов нахождения экстремума функций численными методами.

Постановка задачи: Для функции из лабораторной работы 1 найти экстремальные точки, приняв e=Δ=0.05.

Ход работы:

Метод дихотомии

Начальный этап:

Таблица №1 - Исследуемые точки

Основной этап:

Данная функция:  f(x,y)=x³+2y³

Шаг 1: Вычисляют значения функции в следующих точках: , , где 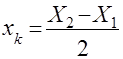, и осуществляют оптимальный выбор:

f()=выбор{f(), f()}.

Находим Хк:

1. 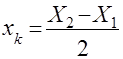   = -0,5

2. 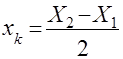 = 0,5

Шаг 2: В зависимости от выбора значения функции изменяют интервал поиска: X₁=выбор{X₁,}; X₂=выбор{,Х2};

1.  х1=-0,5+0,025=-0,475    х2=-0,5-0,025=-0,525

2.  х1=0,5+0,025=0,525      х2=0,5-0,025=0,475

Шаг 3: Далее вычисляем :

1.              -0,525-(-0,475)<=0,05

-0,05<=0,05

2.                0,475-0,525<=0,05

-0,05<=0,05

Если , то конец (как в нашем случае), иначе переход к шагу 1.

Вывод: различные методы нахождения экстремумов функции дают различные результаты. Прежде всего, это связано с тем, что заданную точность для каждого метода стоит задавать отдельно, учитывая особенности каждого метода.