Энтропия и количество информации. Оптимальное кодирование информации. Кодирование последовательностей

этого изучаются основы кодирования и основные области применения кодов.

Цель изучения  дисциплины является усвоение студентами теоретических основ и математического аппарата для описания данных, их преобразования и передачи.

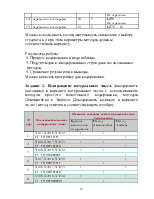
Выполнение практических работ по дисциплине “Математические модели процессов информации и управления” предполагает обучение студентов основам работы с математическими моделями процессов передачи информации; криптографическими методами защиты информации и основам теории графов. В каждой работе приводятся краткие теоретические сведения, необходимые для выполнения работы, с иллюстрациями и примерами. Для каждой работы предусмотрены варианты заданий для выполнения.

Практическая работа № 1 Энтропия и количество информации

Энтропия – степень неопределенности состояния системы.

Пример:

Пусть имеется два дискретных ансамбля     

В дискретном ансамбле y степень неопределенности будет больше.

Собственная информация сообщения xi характеризует информативность или степень неожиданности конкретного ансамбля.

Математическое ожидание этой величины будет характеризовать информативность всего ансамбля. 

Определение:Энтропией дискретного ансамбля Х={xi,p(xi)} называется величина H(x) = M[I(x)] = ∑I(xi)*p(xi) = - ∑p(xi)*logp(xi) 

По определению получается, что энтропия представляет собой среднеожидаемое количество информации от системы.

Свойства энтропии:

1) Неотрицательность H(x)≥0

Энтропия будет равной нулю, если система детерминированная

2) H(x)≤log|x|

Равенство будет иметь место, когда сообщение системы равновероятно.

3) Пусть имеется дискретный ансамбль Х и пусть на множестве его элементов определена некоторая функция q(x), введем дискретный ансамбль Y = {y=q(x)}, тогда для множества Y будет выполняться неравенство H(Y)≤H(X). Это означает, что обработка информации не приводит к увеличению энтропии.

Условная энтропия

Пусть имеются две зависимые системы X и Y . Обозначим p(yj/xi) вероятность того, что система Y примет значение Yj при условии, что система Х приняло значение Xi

P(Yj/Xi) = P(Y=yj, при X=xi).

Условные вероятности должны быть  заданы для всех значений Y и Х. Для их задания используется матрица

p(y1/x1)  p(y2/x2) …p(yn/x1)

……………………………

p(y1/xm) p(y2/xm)…p(yn/xm)          

С помощью матрицы можно посчитать частную энтропию:

H(Y/Xi)=∑p(yj/xi)*log p(yj/xi)

Частную условную энтропию можно выразить через математическое ожидание  H(Y/xi) = M[-log p(Y/xi)].

Чтобы полностью охарактеризовать энтропию системы нужно определить полную или среднюю энтропию. Для этого надо частную условную энтропию усреднить по всем значениям х с учетом вероятности.

Определение: Полная условная энтропия сообщения y относительно х будет величина:

H(Y/X) = ∑p(xi)*H(Y/xi)= -  ∑∑p(xi)*p(yj/xi)*log p(yj/xi)= =∑∑p(xi,yj)*log p(yj/xi)

Понятие условной энтропии используется для определения информационных потерь, при передаче по каналам связи с помехами. В этом случаи система Х соответствует сообщениям источника, система Y – сигналы, принимаемые приемником. Матрица Р(Y/X) характеризует информационные потери, при передаче сообщений xi.

   И                         П

  х1                           y1

  х2                            y2

  хi                            yi  –  p(yi/xi) эта вероятность соответствует правильному приему

xn                            yn

Таким образом, H(Y/xi) характеризует неопределенность того, что, отправив xi, мы получим любой из элементов множества Y.

Матрица, задающая p(yj/xi) называется канальной матрицей.

Рассмотрим приемник, т.е. систему Y. Когда приемник получает сигнал yi, существует неопределенность: какой сигнал был отправлен с источника.

   И                         П

  х1                           y1

  х2                           y2

  хi                            yi

xn                            yn

В этом случае для подсчета энтропии используется канальная матрица P(X/Y). Ей соответствует частная условная энтропия H(X/yi) и полная условная энтропия H(X/Y).

Энтропия сложной системы. Объединение двух систем

X и Y называется сложная система Х и Y, постоянные которой представляют собой все возможные комбинации состоящих Х и Y.

Если система Х={xi,p(xi)}, а система Y={yj,p(yj)},тогда вероятности объединенной системы (х,y) будем обозначать pij=p(xi,yj). Эти вероятности удобно записывать в виде матрицы P(X,Y).

Эта матрица обладает следующими свойствами:

1) ∑∑pij=1

2) pi=∑pij задают распределение состояния системы Х.

pj=∑pij задают распределения системы Y.

Энтропией сложной системы называется величина:

H(X,Y)= - ∑∑pij*log pij

В форме математического ожидания: H(X,Y) = M[-log p(xi,yj)]

Свойства энтропии сложной системы:

1) Если системы Х и Y независимы, тогда

H(X,Y)=H(X)+H(Y)

2) Если Х и Y независимые системы, тогда

Н(X,Y)=H(X)+H(Y/X)

Из свойства 2 вытекает следствие: H(X,Y)=H(Y)+H(X/Y)

3) H(X/Y)≤H(X) и H(Y/X)≤H(Y)

4) H(X,Y)≤H(X)+H(Y)

5) Если системы X и Y эквивалентны, то H(X,Y)=H(X)=H(Y). Системы X и Y эквивалентны, если постоянные одной системы полностью