Где цифра – 1,2 или 3 в зависимости от номера раздела. Фамилия_студента – фамилия и инициалы без пробелов. Желательно английскими буквами.
От каждого студента должно получиться три файла, имена которых отличаются только первой цифрой. Данные файлы переслать (можно в архиве) на ящик pchechet@gsu.by.
Самостоятельно разработать граф из 10 вершин. Соединить их рёбрами так, чтобы получилось три связанных подграфа, не связанных между собой. Каждый студент должен предложить уникальный вариант связи вершин графа. Пример одного из вариантов на рисунке:
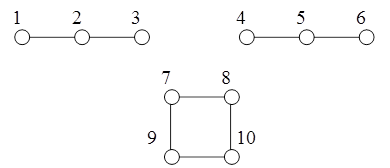
Разработать программу, которая по матрице А смежности графа строит матрицу достижимостей R. Программа должна выводить на экран или в файл исходную матрицу смежности A и вычисленную матрицу достижимостей R.
Разработанный в предыдущей лабораторной работе граф дополнить ребрами так, чтобы он стал связным. Пример на рисунке:
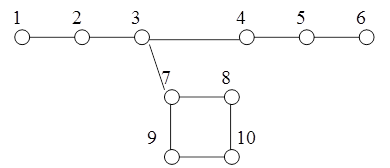
Разработать программу, реализующую алгоритмы просмотра вершин графа поиском в глубину и в ширину. Для каждого их вариантов просмотра вершин программа должна вывести номера вершин и их порядковый номер просмотра. Пример для графа на рисунке, если просмотр начинается с вершины 1:
Поиск в глубину:
№ просмотра: 1 2 3 4 5 6 7 8 9 10
№ вершины: 1 2 3 4 5 6 7 8 10 9
Поиск в ширину:
№ просмотра: 1 2 3 4 5 6 7 8 9 10
№ вершины: 1 2 3 4 7 5 8 9 6 10
Номер вершины, с которой начинается просмотр, должен задаваться пользователем.
Разработать программу построения каркаса (стягивающего дерева), для графа методами поиска в глубину и поиска в ширину c выбираемой пользователем вершины. Модифицировать (добавить новые и/или удалить старые) рёбра графа из предыдущей лабораторной работы так, чтобы получаемые разными методами каркасы различались. В отчёте изобразить полученные каркасы на рисунках.
Реализовать программы построения каркаса минимального веса методами Краскала и Прима. За основу взять граф из предыдущей лабораторной работы, рёбра которого нужно нагрузить положительными значениями. Программа построения графа методом Краскала должна помимо ребёр каркаса выводить исходный массив весов ребёр графа. Программа построения каркаса методом Прима должна выводить исходную матрицу смежности графа. Каждая программа должна подсчитывать и выводить вес получившегося каркаса. В отчёте представить исходный граф и получившиеся каркасы минимального веса на рисунках.
Граф из работы №6 дополнить рёбрами так, чтобы степень каждой вершины оказалась чётной. Разработать программу, реализующую поиск Эйлерового цикла с использованием рекурсивного поиска в глубину. Исходная вершина должна выбираться пользователем. В отчёте отобразить найденный цикл на рисунке.
Рёбра в графе из работы №6 нужно нагрузить натуральными числами – пропускной способностью между вершинами, также выбрать направление ребёр. Можно при необходимости добавить новые рёбра и удалить старые.
Разработать программу, реализующую алгоритм Форда-Фалкерсона для нахождения максимального потока между двумя разными вершинами, номера которых вводятся пользователем. Помимо значения величины потока программа должна выводить и распределение потока по рёбрам графа. В отчёте представить исходный граф с пропускными способностями и один из вариантов распределения максимального потока для некоторых вершин.
Предложить некоторый правдоподобный технологический процесс: ремонт, изготовление, постройка, тестирование и др. некоторого объекта, процесса, изделия и др.
Перечислить список работ проекта (6 и больше) и изобразить в отчёте их порядок выполнения с помощью ориентированного графа с использованием модели «работы–дуги». Для каждой работы предложить правдоподобное время её выполнения. Разработать программу, определяющую и выводящую критическое время выполнения проекта и критический путь. Также для всех событий программа должна вычислять и выводить ранние и поздние времена наступления событий. На основании этих времён программа должна вычислять и выводить полный и свободный резервы времени для всех работ проекта.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.