Предупреждение распространения пожара при разрушении технологического оборудования

решения этой задачи рассмотрим процессы возникновения и распространения волны прорыва, образующейся при разрушении РВС и ее взаимодействия с защитными преградами.

Для волны прорыва свойственны наличие резкого фронта в виде бора (вала), достигающего значительной высоты и движущегося с большой скоростью, а также большая разрушительная сила потока. При этом типе движения профиль волны имеет резко выраженную кривизну линий тока, изменение которой, как правило, столь круто, что профиль потока по существу разрывается, приходя в состояние высокой турбулентности. Следовательно, вертикальный компонент ускорения играет здесь значительную роль, тогда как влиянием трения в канале практически можно пренебречь по сравнению с динамическим эффектом движения потока.

Характерными особенностями этого вида движения являются:

- кривизна потока, которая выражена настолько резко, что распределение давления не может быть принято гидростатическим;

- быстрое изменение режима потока происходит на относительно коротком участке, поэтому граничное трение, как правило, ничтожно;

- при возникновении быстро изменяющегося движения в резких переходных сооружениях физические характеристики потока определяются в основном геометрией границ сооружения и состоянием потока.

Основным способом решения задачи, связанной с образованием волны прорыва при внезапном разрушении водохранилища и распространением ее в широком прямоугольном русле с постоянным уклоном, являются методы вычислительной гидравлики, использующие дифференциальные уравнения Сен-Венана [7] вида

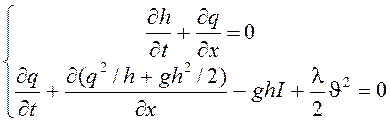,                                    (9.1)

где     h – глубина потока; q – расход на единицу ширины;  - скорость течения; I – уклон дна русла; t – время; x – пространственная переменная;  - коэффициент гидравлического трения.

Уравнения (9.1), в данном случае, приведены в виде законов сохранения массы и импульса. Такая форма записи уравнений позволяет считать обобщенными решениями системы разрывные решения, удовлетворяющие соответствующим законам сохранения в интегральной форме и включающими гидравлические прыжки и боры.

Решение задачи о неустановившемся движении жидкости в открытом русле сводится к интегрированию уравнений Сен-Венана или их модификаций. В результате должны быть получены две функции Q = Q(t, l) и w = w(t, l), зная которые можно найти изменение расхода во времени в любом створе потока и построить мгновенный профиль свободной поверхности в любой момент времени. Однако дифференциальные уравнения Сен-Венана являются нелинейными и их интегрирование в общем случае невозможно. Поэтому на практике применяются методы приближенного (численного) интегрирования с использованием ЭВМ, решения которых, вследствие их ограниченной точности, необходимо тестировать путем сравнения результатов численных вычислений с натурными данными или результатами лабораторных опытов.

Математическая модель возникновения и распространения волны прорыва, образующейся при разрушении РВС, а также ее взаимодействия с защитной преградой разработана на основании известных теоретических положений о неустановившихся гидродинамических явлениях совместно с кафедрой нефтегазовой гидродинамики Академии нефти и газа им. И.М. Губкина [8].

Рассматривалось движение слоя жидкости глубиной  по плоскости, наклоненной к горизонту под углом , которое характеризовалось осредненными по высоте слоя компонентами скорости , соответственно вдоль осей 0Х и 0Y. Жидкость предполагалась несжимаемой, поэтому уравнение неразрывности, проинтегрированное по высоте слоя приводило к уравнению, связывающему эту высоту с осредненными компонентами скорости течения

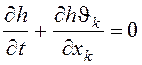,                                             (9.2)

Под повторяющимся индексом  подразумевали суммирование от 1 до 2.

Поскольку основными факторами, определяющими развитие волны прорыва, являются сила тяжести и инерции жидкости, в уравнениях движения трением пренебрегали, а в качестве движущей силы приняты горизонтальные составляющие градиента гидростатического давления, обусловленного непостоянством глубины слоя жидкости. В этом случае имели

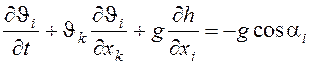,                              (9.3)

где   – ускорение силы тяжести;  – углы, образованные вектором скорости и направлением силы тяжести.

В одномерной задаче, моделирующей распространение жидких лавин при разрушении стенок плоского канала или резервуара, система определяющих уравнений (9.2) и (9.3) упрощалась

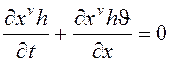
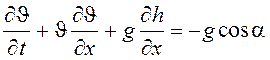.                   (9.4)

Входящий в нее индекс  равен 0 или 1 в зависимости от того. плоская или цилиндрическая симметрия рассматривалась.

Рассматриваем плоскую задачу: между двумя створами  имеется бесконечный канал, заполненный жидкостью с постоянной глубиной Н_о. В начальный момент времени  створы мгновенно разрушаются и покоящаяся до того жидкость приходит в движение, растекаясь в обе стороны. На расстояниях  справа и слева от створов канала, то есть в точках , расположены защитные стенки, препятствующие проникновению жидкости в область > L. Необходимо найти высоту стенок с учетом того обстоятельства, чтобы жидкая лавина не смогла их преодолеть. Ответ на этот вопрос может быть найден из решения следующей краевой задачи:

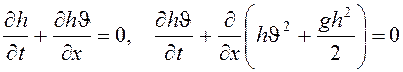
                                                                                                                   (9.5)

При этом высота Н_с защитных стенок находится как максимальная высота