




Найти оптимальное значение частоты изменения силы резания. Вызывающее минимальное влияние рассматриваемого станка на соседнее оборудование.
Действующие элементы упругости и деформирования сведем к 2-м. Для этого определяем силы реакции и попарно их суммируем.
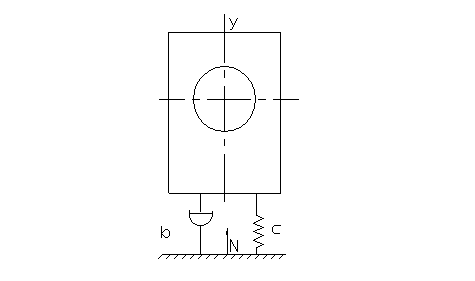
![]() (1)
(1)
Будем искать решение дифференциального уравнения в виде синусоиды.
![]() (2)
(2)
![]() (3)
(3)
(2),(3)→(1)
=>
![]() (4)
(4)
Исходя
из условий задачи, стремимся к минимальному значению функции N. Для этого приравниваем ее первую производную к нулю.![]()
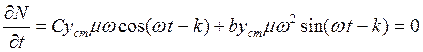 (5)
(5)
Для упрощения полученного выражения введем обозначения:
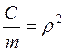 ;
; 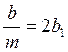 ;
;
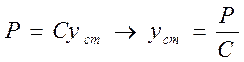
Подставим принятые обозначения в (4) и (5).
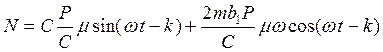
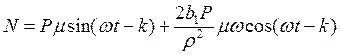
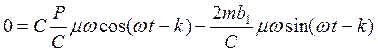
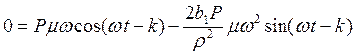
Возведем уравнения в квадрат:
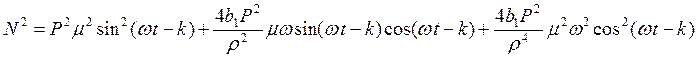
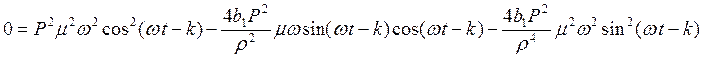
Сократим
на ![]() и упростим:
и упростим:
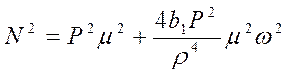
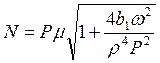
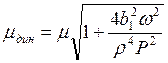
РИС
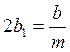 ;
; 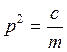
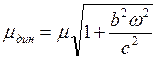
Полученная зависимость позволяет правильно определить суммарную жесткость опоры и связь между суммарной жесткостью станка и фундамента.
Анализ
полученного графика позволяет заключить, что при значении отношения ![]() действительная нагрузка
прямопропорционально передается на пол и соседнее оборудование. При увеличении
этого соотношения происходит уменьшение передаваемой нагрузки, т.е. снижение
частоты и амплитуды колебаний. Это связано с влиянием сил инерции оборудования.
действительная нагрузка
прямопропорционально передается на пол и соседнее оборудование. При увеличении
этого соотношения происходит уменьшение передаваемой нагрузки, т.е. снижение
частоты и амплитуды колебаний. Это связано с влиянием сил инерции оборудования.
Моделирование тепловых задач
и моделирование методом размерности.
1.Метод размерности.
При моделировании численными методами (мет. конечных элементов, граничных элементов) крупных габаритных деталей приходится решать систему большой размерности.
Для уменьшения этой размерности создаются расчетные или технические модели. Для сопоставления полученных результатов используются безразмерные критерии, которые можно получить методом размерности.
Пример:
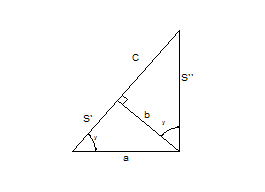
[c]=L; [φ]=рад (безразмерная величина)
Площадь S:
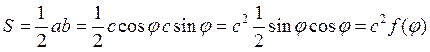
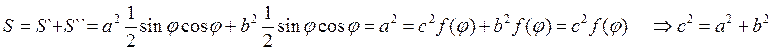
Пример2:
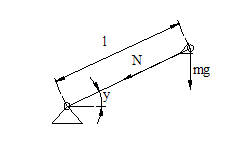
1. Выделяем все учитываемые параметры расчетной схемы: l;φ;N;m;g;t.
φ – безразмерный параметр.
2. Используем второе уравнение размерности.
Для этого выделенные параметры возводим в произвольную степень. Произведение этих параметров должно быть равно единице.
Определяем размерность параметров. Переписываем уравнение в размерностях. Так как произведение степенных функций равно 1, то их показатели должны равняться 0.
3. Приравняв к нулю показатели, определяем их выражения.
[l]≡L; [N]≡F; [m]≡M; [q]≡LT-2; [t]≡T
Основное уравнение:
![]()
![]() (1)
(1)
![]()
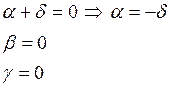
![]()
Присваиваем любое значение:
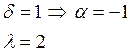 (2)
(2)
(2)→(1)
=> 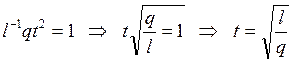
![]() – безразмерный
параметр.
– безразмерный
параметр.
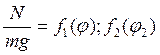 (3)
(3)
(3) – позволяет заключить, что для эквивалентности модели и натурного образца необходимо чтобы были эквивалентны безразмерные критерии.
1- одинаковые углы φ
2- одинаковые или пропорциональные размеры l.
Если необходимо учесть физико-механические свойства материала руки, заготовки, то добавляем параметры: Е – модуль упругости, μ – коэффициент Пуассона.
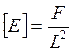 Перепишем это равенство в физических величинах.
Перепишем это равенство в физических величинах.
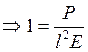 - безразмерный
критерий.
- безразмерный
критерий.
Если в рассматриваемой модели нужно было бы оценить внутреннее напряжение, то нужно ввести параметр σ.
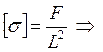 еще один
безразмерный критерий.
еще один
безразмерный критерий.
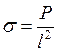 (4) -
показывает, что напряжения, возникающие в модели будут эквивалентны напряжениям
в натуральном образце, в том случае когда будет соблюдаться соотношение:
(4) -
показывает, что напряжения, возникающие в модели будут эквивалентны напряжениям
в натуральном образце, в том случае когда будет соблюдаться соотношение:
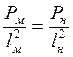 (5)
(5)
Условие (5) позволяет найти длину модели.
2. Метод тепловых задач.
РИС
Рассмотрим участок (i,j;i-1,j)
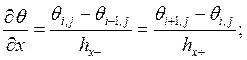 (1) – выражение
первой производной в конечных разностях.
(1) – выражение
первой производной в конечных разностях.
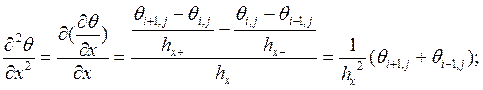 (2)
(2)
Так как выражение торой производной зависит от нумерации точек, то конечную разность с шагом назад поменяем местами с конечной разностью шагом вперед.
(1)→(2)=> 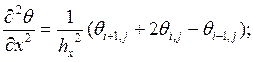
Если вместо hx взять время:
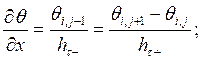
Пример:
Рассмотрим круговой стол станка.
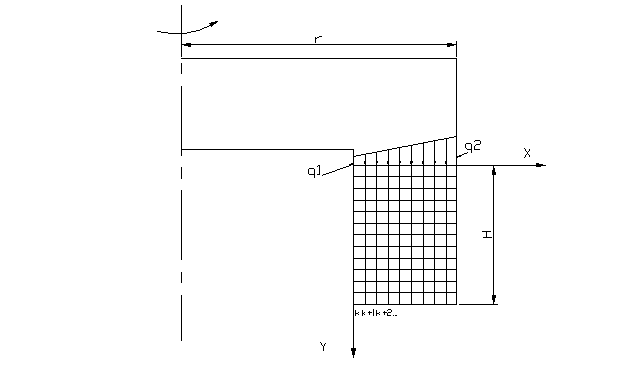
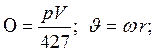
Разбиваем схему на квадраты.
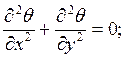
Уравнение теплопроводности для этой задачи.
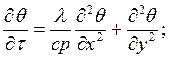
Перепишем уравнение в конечных разностях.
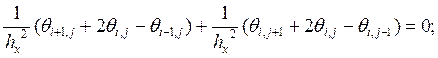
Для одного из квадратов:
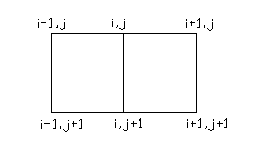
Для решения системы добавим граничные условия.
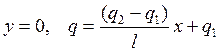 => известен
закон теплового потока по длине.
=> известен
закон теплового потока по длине.
Для адиабатической границы:
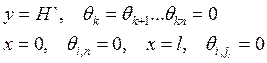
Решив совместно уравнения с граничными условиями, получаем температуру в узловых точках.
Недостаток заключается в том, что всю область необходимо разделить на одинаковые квадраты и количество уравнений получается очень большим ( сколько квадратов столько и уравнений). Этот недостаток можно уменьшить используя метод конечных элементов или метод граничных элементов.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.