 ка, то распределение
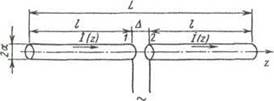
токов на плечах вибратора получается таким, что полное электрическое поле
удовлетворяет граничному условию Е = 0, где т —касатсльная компонента к
поверхности Рис. 2 1 вибратора. Строгое решение за-
ка, то распределение
токов на плечах вибратора получается таким, что полное электрическое поле
удовлетворяет граничному условию Е = 0, где т —касатсльная компонента к
поверхности Рис. 2 1 вибратора. Строгое решение за-
Рис. 2.2
дачи нахождения тока, несмотря на простоту геометрии задачи, встречает большие математические трудности (см. 2.4). Приближенная теория электрических вибраторов из тонких проводов основана на аналогии с длинной линией.
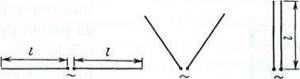 |
Используем второй способ. В разомкнутой линии без потерь распределение тока вдоль линии представляется суперпозицией двух бегущих волн: падающей и отраженной, амплитуды которых равны. При наличии потерь амплитуда падающей волны в каждой точке преобладает над амплитудой отраженной волны; в распределении тока теперь отсутствуют нулевые значения. Функция распределения тока при этом описывается выражением [37]
j(z) = —shy(/ — г), (2.1)
shy/ где 4 — ток на входе линии; у = (х + Щ, а — коэффициент затухания, [3 — коэффициент фазы; — координата, отсчитываемая вдоль линии от вход-
 ных точек (рис. 2.3).
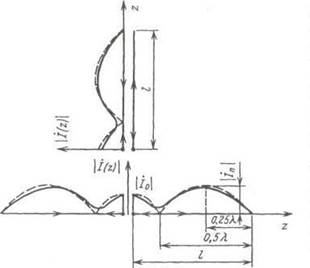
Методика расчета коэффициентов сх и [З дана ниже (см. 2.3). На рис. 2.3
сплошной линией изображено характерное распределение модуля тока в
эквивалентной разомкнутой линии, описываемого формулой (2.1), а также вдоль
плеч вибратора, получаемого путем обратного развертывания проводников
эквивалентной лиНИИ. Отметим, что для вибраРис. 2.3 тора ввиду симметрии
картины тока относительно точек питания в (2.1) необходимо ввести
ных точек (рис. 2.3).
Методика расчета коэффициентов сх и [З дана ниже (см. 2.3). На рис. 2.3
сплошной линией изображено характерное распределение модуля тока в
эквивалентной разомкнутой линии, описываемого формулой (2.1), а также вдоль
плеч вибратора, получаемого путем обратного развертывания проводников
эквивалентной лиНИИ. Отметим, что для вибраРис. 2.3 тора ввиду симметрии
картины тока относительно точек питания в (2.1) необходимо ввести
j(z) = —shy(/— 21). (2.2)
На концах тонкого вибратора ток всегда равен нулю; другие нулевые значения, как уже отмечалось, отсутствуют. В любых двух точках, симметричных относительно = О, направление тока одинаково.
При расчете ДН функцию распределения тока можно еще более упростить, пренебрегая затуханием, т.е. полагая = 0, = К, где К = = 2л,Оч — коэффициент фазы в свободном пространстве. В этом случае shy(/ — ) = sink(/ — ) и распределение тока описывается функцией
![]() (2.3) sink/
(2.3) sink/ ![]() соответствующей чисто
стоячей волне с нулевым значением на концах антенны (узел тока); при узлы и
пучности чередуются через )Ј4. Кривая распределения тока, соответствующая
(2.3), показана штриховой линией на рис. 2.3. Переходу i через нуль в этом
случае соответствует изменение фазы тока на противоположное, что отажено
соответствующими стрелками на рис. 2.3. Как видно, отличие i(z) от кривых,
соответствующих более точному выражению (2.2),
соответствующей чисто
стоячей волне с нулевым значением на концах антенны (узел тока); при узлы и
пучности чередуются через )Ј4. Кривая распределения тока, соответствующая
(2.3), показана штриховой линией на рис. 2.3. Переходу i через нуль в этом
случае соответствует изменение фазы тока на противоположное, что отажено
соответствующими стрелками на рис. 2.3. Как видно, отличие i(z) от кривых,
соответствующих более точному выражению (2.2),
невелико и наблюдается только в области вблизи нулевых значений. Соответственно погрешность расчета ДН по распределению тока (2.3) будет также невелика и определяется в первом приближении разницей площадей под кривыми тока. Обратим внимание, что при = п)Ј2 , где п = 1, 2, З, ... знаменатель в (2.3) обращается в нуль. В этом случае вводят понятие тока в пучности (термин из теории длинных линий), который всегда отличен от нуля. Поскольку 4 = /o/sinkt, то вместо (2.3) можно использовать i(z) = fnsink(l— lzl). (2.4)
![]() Кроме распределения тока представляет интерес вопрос о
распределении зарядов вдоль вибратора, важный для определения предельной
мощности, которую можно подвести к вибратору, не опасаясь пробоя. Используя
уравнение непрерывности [ 18] и учитывая, что ток в тонком вибраторе имеет
только продольную составляющую, получаем dj(z) (2.5)
Кроме распределения тока представляет интерес вопрос о
распределении зарядов вдоль вибратора, важный для определения предельной
мощности, которую можно подвести к вибратору, не опасаясь пробоя. Используя
уравнение непрерывности [ 18] и учитывая, что ток в тонком вибраторе имеет
только продольную составляющую, получаем dj(z) (2.5)
dz где 0(z) — заряд на единицу длины. Из
(2.5) и (2.4) следует, что приближенный закон распределения плотности зарядов
описывается выражением ф(г) = ![]() lzl), (2.6)
lzl), (2.6)
причем знак плюс относится к точкам > 0,
минус — к точкам 2 < 0, ![]() = /с, с — скорость света. Как следует из
(2.6), на концах вибратора всегда имеет место пучность зарядов; узлы и пучности
зарядов чередуются, как и ток, через i/4.
= /с, с — скорость света. Как следует из
(2.6), на концах вибратора всегда имеет место пучность зарядов; узлы и пучности
зарядов чередуются, как и ток, через i/4.
Отметим, что при несимметричном возбуждении вибраторов распределение тока и зарядов существенно меняется, но для вибраторов резонансной длины, т.е. при = п)Ј2, п = 1, 2, З остается неизменным.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.