










точках интерференционных минимумов модуль множителя ослабления уменьшается до величины
min![]() (16.20) где R — модуль коэффициента
отражения при . В этих точках vmin < 1.
(16.20) где R — модуль коэффициента
отражения при . В этих точках vmin < 1.
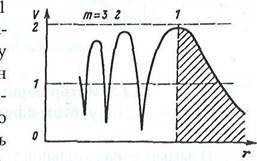 На рис. 16.8 показана зависимость V(r). Как видно из
рисунка, ширина интерференционных лепестков уменьшается по мере приближения к
источнику, что согласно (16.14) объясняется гиперболической зависимостью
разности хода дг от расстояния. Одновременно значения [7 в точках минимумов
возрастают, поскольку при приближении к источнику углы д увеличиваются, а
значения R уменьшаются (см. рис. 16.4). В первом интерференционном максимуме,
который соответствует т = и располагается на наибольшем удалении от источника,
сдвиг фаз между прямой и отраженной волнами равен 2п. При дальнейшем удалении
от источника траектории волн настолько сливаются, что дг —» 0 и множитель
ослабления уменьшается монотонно.
На рис. 16.8 показана зависимость V(r). Как видно из
рисунка, ширина интерференционных лепестков уменьшается по мере приближения к
источнику, что согласно (16.14) объясняется гиперболической зависимостью
разности хода дг от расстояния. Одновременно значения [7 в точках минимумов
возрастают, поскольку при приближении к источнику углы д увеличиваются, а
значения R уменьшаются (см. рис. 16.4). В первом интерференционном максимуме,
который соответствует т = и располагается на наибольшем удалении от источника,
сдвиг фаз между прямой и отраженной волнами равен 2п. При дальнейшем удалении
от источника траектории волн настолько сливаются, что дг —» 0 и множитель
ослабления уменьшается монотонно.
Рис. 16 8
На стационарных наземных радиолиниях, работающих в пределах освещенной зоны, пункт приема обычно располагают вблизи псрвого интерференционного максимума.
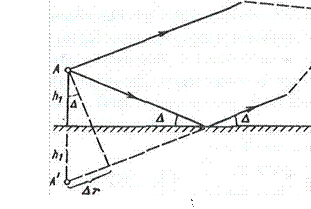
Из формулы (16.15) видно, что интерференционная структура поля имеет место не только вдоль трассы, но и по высоте. Это можно трактовать как влияние Земли на диаграмму направленности передающей антенны. Для оценки этого влияния выразим разность хода лучей = 2/1 sinA (рис. 16.9). Подставив это соотношение в (16.12), получим
У = 1+R2 /i)sinA-O]. (16.21)
Из формулы видно, что в результате влияния Земли диаграмма направленности излучателя приобрела многолепестковый характер. При углах д, соответствующих (4Tthl/i)sinA — = 2тп, т = 0, 1, 2, ... , множитель ослабления V максимален и равен I + R. При углах д, соотвстствующих
(47thl/i)sinA — 0 = (2n + l)7t, у = 0, 1,
2, .![]()
множитель ослабления И минимален и равен — R.
16.2.3. Интерференционный множитель с учетом сферичности Земли
В рамках отражательной трактовки, когда влияние Земли сводят к интерференции в точке приема прямой и отраженной волн, влияние сферичности земной поверхности учитывают путем соответствующих изменений амплитуды и фазы отраженной волны по сравнению со случаем плоской Земли.
Начнем с вопроса о фазовых соотношениях. При сферической земной поверхности сдвиг фаз полей прямой и отраженной от Земли волн в точке приема удобно выразить в виде функции не- Рис. 16.10 которых высот, которые называются приведенными высотами и обозначаются 1' и h2'. Для определения этих высот необходимо провести плоскость S, касательную к сферической земной поверхности в точке отражения С (рис. 6.10). Тогда разность хода — rl над сферической поверхностью будет равна разности хода над плоскостью S и может быть рассчитана через высоты hI' и 112', отсчитываемые от плоскости S
Из рис. 16.10 следует, что
![]() (16,22)
(16,22)
Согласно определению предельного расстояния прямой видимости (16.1) длина участков r' — 2азмД/11 И 2а зм 2 следовательно,
![]() (16.23)
(16.23)
Определение местоположения точки отражения на трассе, т. е. определение r' и Р' в случае произвольного соотношения высот h и довольно громоздкая задача. Приближенно r' = rhl/(hl + h2); К' = rh2/(hl + h2). (16.24)
Подставляя в (16.22) выражения (16.23) и (16.24), получаем
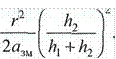
 2
2
• h'2 =h2-(16.25)
Точный расчет приведенных высот рассмотрен
в [28].![]()
Зная приведенные высоты (16.25), разность хода прямой
и отраженной волн для сферической Земли определяется как ![]() дг = 2/11'h2'/r. (16.26)
дг = 2/11'h2'/r. (16.26)
После замены истинных высот hl и h2 на приведенные hl' и h'2 угол д (см. рис. 16.7) определяются как tgA sinA = (h'l + h2')/r. (16.27)
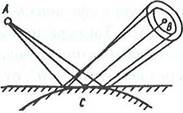 Выпуклость земной поверхности приводит к заметному
расхождению отраженной волны (рис. 16.11), что уменьшает плотность пото
Выпуклость земной поверхности приводит к заметному
расхождению отраженной волны (рис. 16.11), что уменьшает плотность пото![]() ка
мощности отраженной волны в заданном направлении. Для учета
ка
мощности отраженной волны в заданном направлении. Для учета ![]() этого явления
вводят понятие коэффициента расходимости. Если обозначить через
этого явления
вводят понятие коэффициента расходимости. Если обозначить через ![]() площадь сечения
телесного угла пучка волн, отраженных в пределах плоской существенной области
для отражения, а через ,Sc4) — то
площадь сечения
телесного угла пучка волн, отраженных в пределах плоской существенной области
для отражения, а через ,Sc4) — то ![]() же, для случая сферической поверхности, то
изменение плотности потока будет пропорРис. 16.11 ционально отношению
площадей [ЖКХф, а изменение напряженности поля —
же, для случая сферической поверхности, то
изменение плотности потока будет пропорРис. 16.11 ционально отношению
площадей [ЖКХф, а изменение напряженности поля —
 (16.28)
(16.28)
Уменьшение напряженности поля отраженной волны за счет расхождения пучка лучей оценивают путем изменения модуля коэффициента отражения :
![]() (16.29) сф
(16.29) сф
После подстановки в (16.12) величин (16.26) и RCф (16.29),
получаем выражение для модуля интерференционного множителя ![]() с учетом
сферичности Земли:
с учетом
сферичности Земли:
(16.30)
а действующее значение напряженности поля
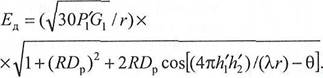 (16.31)
(16.31)
![]()
![]()
![]()
![]()
![]()
![]() Предел применимости интерференционного множителя (16.30)
на трассах, протяженность которых нс превышает предельного расстояния прямой
видимости (16.1), обусловлен тем, что отражательная трактовка, заложенная в
основу этой формулы, предполагает наличие двух волн в точке приема — прямой и
отраженной. Специальные расчеты [59] показывают, что представление
Предел применимости интерференционного множителя (16.30)
на трассах, протяженность которых нс превышает предельного расстояния прямой
видимости (16.1), обусловлен тем, что отражательная трактовка, заложенная в
основу этой формулы, предполагает наличие двух волн в точке приема — прямой и
отраженной. Специальные расчеты [59] показывают, что представление
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.