






















ВВЕДЕНИЕ
Редуктором называют механизм, состоящий из зубчатых или червячных передач, выполненный в виде отдельного агрегата и служащий для передачи мощности от двигателя к рабочей машине.
Назначение редуктора – понижение угловой скорости и повышение вращающего момента ведомого вала по сравнению с валом ведущим.
В данной работе нам необходимо будет спроектировать цилиндрический одноступенчатый редуктор, а так же привод цепного транспортера.
1. Кинематический расчет привода.
1.1 Подбор электродвигателя [2, стр.5]:
Потребляемую мощность (кВт) привода (мощность на выходе) Рв определяют по формуле:
![]() ,
,
![]() .
.
Тогда требуемая мощность электродвигателя:
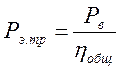 , где ηобщ – коэффициент
полезного действия (КПД) привода.
, где ηобщ – коэффициент
полезного действия (КПД) привода.
Определяем КПД привода [2,стр.5]:
hоб =hм·hз×h3п ×ηцеп
hм - КПД муфты, hм=0,98;
hз -КПД зубчатой передачи, hз=0,97;
hп - КПД подшипников,hп=0,99;
ηцеп – КПД цепной передачи, ηцеп=0,93;
![]()
Определяем требуемую мощность на валу электродвигателя:
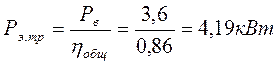
Требуемая частота вращения вала электродвигателя:
![]() ,
,
Частота вращения приводного вала, мин-1 [2, c. 5]:
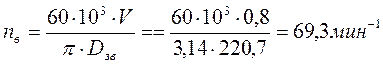
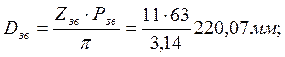
![]()
Определяем требуемую частоту вращения вала электродвигателя:
![]() .
.
По табл. 24.9 [1] подбираем электродвигатель с требуемой мощностью Рэ.тр = 4,19 Вт и частотой вращения ротора n’дв = 866,25 мин-1. Указанным условиям удовлетворяет двигатель серии : АИР 132М8/720 с мощностью P = 5,5 кВт, асинхронной (номинальной) частотой вращения n = 720 мин-1.
1.2 Определение передаточных чисел привода [2,стр. 6].
После окончательного определения частоты вращения вала двигателя определяют общее передаточное число привода.
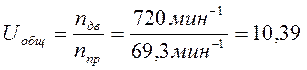
Общее передаточное число также определяется по формуле:
![]()
![]() Uцеп=2,5;
Uцеп=2,5; 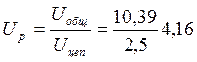
1.3 Определение вращающих моментов на валах:
Вращающий момент на валу электродвигателя:
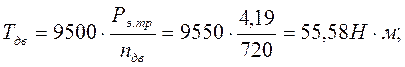
Вращающий момент на быстроходном валу, Н·м:
![]()
Вращающий момент на тихоходном валу, Н·м:
![]()
Вращающий момент на приводном валу, Н·м:
![]()
2. Расчёт цилиндрической передачи.
2.1 Выбор материала и определение допускаемых напряжений:
Назначаем для зубчатых колёс Сталь 45 с термообработкой улучшение.
Твёрдость зубьев на поверхности
а) шестерни: 269…302 НВ,
б) колеса: 235…268 НВ,
Принимаем для шестерни – 285,5 НВ, для колеса – 251,5 НВ.
2.2 Допускаемые контактные напряжения:
Допускаемые контактные напряжения при расчетах на прочность определяются:
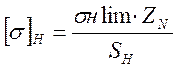
![]() - предел
выносливости для углеродистых и легированных сталей, определяется по таблице [2,стр.
9, таблица 5]
- предел
выносливости для углеродистых и легированных сталей, определяется по таблице [2,стр.
9, таблица 5]
![]() =2НВср+70=2∙285,5+70=641МПа,
=2НВср+70=2∙285,5+70=641МПа,
![]() =1,75НВср=1,75∙285,5=499,63МПа,
=1,75НВср=1,75∙285,5=499,63МПа,
Величина Zн – коэффициент долговечности, учитывающий влияние срока службы и режима нагрузки передачи:
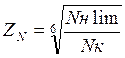 , где Nнlim – базовое число циклов,
определяется в зависимости от средней твердости поверхности зубьев по таблице [2,
стр.9, таблица 6]
, где Nнlim – базовое число циклов,
определяется в зависимости от средней твердости поверхности зубьев по таблице [2,
стр.9, таблица 6]
Nнlim(для шестерни)=25млн. циклов
Nнlim(для колеса)=17млн. циклов
Величина Nk- расчетное число циклов перемены напряжений за весь срок службы: Nk=60·n·с·Lh, где n – частота вращения мин-1 , с- число зацеплений зуба шестерни или колеса за один оборот (с=1), Lh =18000– ресурс передачи:
![]() циклов
циклов
![]()
Sн – минимальный коэффициент запаса прочности[2,стр.10];
Sнa=1,1
Для шестерни:
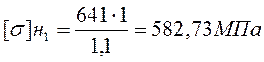 ;
;
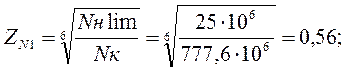 принимаем ZN1= ZN2=1.
принимаем ZN1= ZN2=1.
Для колеса:
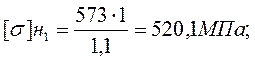
Проверка: ![]() ;
;
![]()
![]()
![]()
Для данной цилиндрической передачи условие выполняется.
2.3 Допускаемые напряжения изгиба[2,стр. 10]:
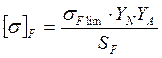 , где
, где
YA- коэффициент, учитывающий влияние двустороннего приложения нагрузки, YA=1(при одностороннем приложении нагрузки)
SF- коэффициент запаса прочности , SF=1,7
YN-коэффициент долговечности(1≤YN≤4):
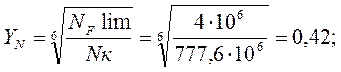
YNа =1, т.к. Nкa>NFlim a
Для шестерни:

Для колеса:
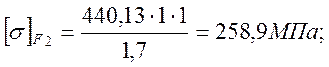
3.Расчёт цилиндрической зубчатой передачи.
3.1 Предварительное значение межосевого расстояния:
 ,[1] где
К- коэффициент межосевого расстояния для шевронных колёс равен 43.
,[1] где
К- коэффициент межосевого расстояния для шевронных колёс равен 43.
Ψа – коэффициент ширины, принимают в зависимость от положения колёс относительно опор, для шевронных колёс Ψа=0,4.
Кнβ – коэффициент концентрации нагрузки. Если скорость колеса меньше 15 м/с, то зубья колёс полностью прирабатываются и Кнβ=1,0.
 , по таблице стандартов принимаем межосевое расстояние
равным 120 мм.
, по таблице стандартов принимаем межосевое расстояние
равным 120 мм.
3.2 Предварительные основные размеры колеса.
Делительный диаметр колеса:
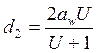 ;
; 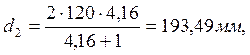
Ширина колеса:
![]()
для шевронных колёс ширина определяется по формуле: b1=b2+1,5∙m =48+1,5∙1,5=50,25мм.
3.3 Модуль передачи.
Сначала принимают коэффициент модуля Кm, для шевронных колёс равный 5,2.
Предварительно модуль передачи: 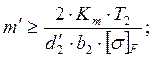
![]() подставляется наименьшее из
двух вышеуказанных.
подставляется наименьшее из
двух вышеуказанных.
 , по
таблице принимаем модуль m=1,5 (мм) – первый ряд.
, по
таблице принимаем модуль m=1,5 (мм) – первый ряд.
3.4 Суммарное число зубьев и угол наклона зубьев
Минимальный угол наклона зубьев шевронных колес: ![]() .
.
Суммарное число зубьев:
![]()
![]()
Действительное значение угла![]() наклона зуба:
наклона зуба:
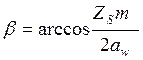 ;
;
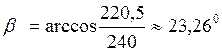
3.5 Число зубьев шестерни и колеса:
- для шестерни:
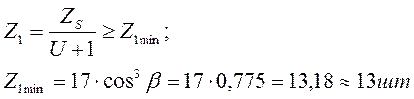
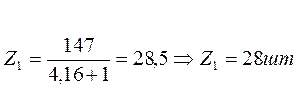
- для колеса:
![]()
3.6 Фактическое передаточное число:
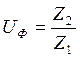
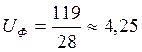
Отклонение от заданного передаточного числа определяется по формуле:
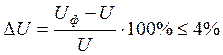
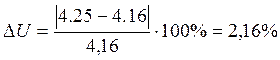 расхождение
меньше 4% является допустимым.
расхождение
меньше 4% является допустимым.
3.7 Размеры колёс:
Делительный диаметр шестерни:
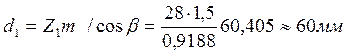
- колеса внешнего зацепления:
![]()
![]()
3.8 Диаметры окружностей вершин da и впадин зубьев df:
Для шестерни: ![]()
![]()
Для колеса: ![]()
![]()
Шевронные зубчатые колёса отличаются от других цилиндрических колёс большей шириной. Наиболее часто шевронные колёса изготавливают с канавкой по середине, предназначенной для выхода фрезы, нарезающей зубья. Ширину канавки (а) определяют по диаметру фрезы в зависимости от модуля. Если m ≤ 2, то (а) принимаем равной 32 мм.
Дополнительные расчёты для шевронного колеса:
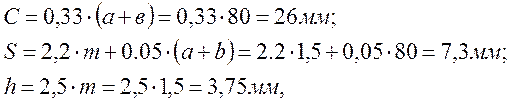
h - высота канавки.
Ширина шестерни: ![]() c учётом особенности колес:
c учётом особенности колес: ![]() для определения ширины колеса
используем соотношение:
для определения ширины колеса
используем соотношение: 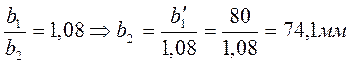 .
.
3.9 Силы в зацеплении:
Окружная сила
![]() ;
;
Радиальная сила:
![]() ,
где α=200,tgα=0,364:
,
где α=200,tgα=0,364: ![]() Осевая
сила:
Осевая
сила:
![]() ,
,
![]()
3.10 Расчетное напряжение изгиба в зубьях.
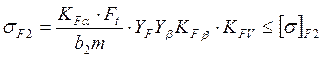 ,
где
,
где
![]() -
коэффициент, учитывающий форму зуба и концентрацию напряжений, принимают по
условию:
-
коэффициент, учитывающий форму зуба и концентрацию напряжений, принимают по
условию: 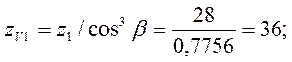
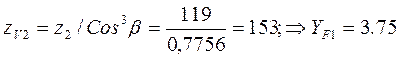 ,
,![]()
![]() коэффициент, учитывающий угол наклона зубьев,
коэффициент, учитывающий угол наклона зубьев, 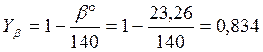 ,
,
![]()
![]() - коэффициент определяется в
зависимости от β и от степени точности, 1.
- коэффициент определяется в
зависимости от β и от степени точности, 1.
![]() - при твёрдости зубьевНВ
более 350 коэффициент определяется:
- при твёрдости зубьевНВ
более 350 коэффициент определяется:
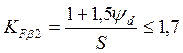 ,
S – индекс схемы, равен 8.
,
S – индекс схемы, равен 8.
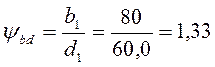 - коэффициент ширины.
- коэффициент ширины.
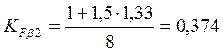 ,
для точного определения коэффициента определяем скорость колеса
,
для точного определения коэффициента определяем скорость колеса
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.