Магнитодвижущая сила катушки обмотки статора. Закон полного тока. Число витков катушки. Удельная проводимость воздушного зазора

Магнитодвижущая сила катушки обмотки статора

Пусть m_СТАЛИ=¥, т.е. магн. сопротивление = 0 (участков, проходящ. по статору и ротору сердечников). Тогда можно считать, что d – величина воздушного зазора и поле будет распространяться равномерно.

i_к=I_mк·sin(wt);

Fкм – амплитудное значение мдс, необходимое для проведения потока через зазор в одном направлении.

t - полюсное деление, Т_п – пространственный период.

 (в пред. лекции)

Возьмём в качестве контура обхода любую силовую линию и применим закон полного тока.

, т.к. в качестве контура обхода – силовая линия, то a = 0; cos a = 1.

, где H_d – вектор напр. в воздушном зазоре.

W_к – число витков катушки. Вместо åi  - мдс.

Мдс, необх. Для проведения потока через зазор в одном направлении:

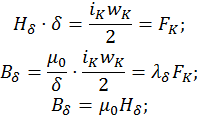
- удельная проводимость воздушного зазора.

Т.к. ток i_к изменяется во времени по синусоидальному закону, то кривая распределения мдс вдоль зазора, сохраняя прямоугольную форму, будет изменяться по амплитуде во времени по синусоидальному закону. Такую мдс и создаваемое ею поле называют пульсирующим.

При анализе мдс машин переменного тока, кривую мдс машин прямоугольной формы разлагают в ряд пространственных гармонических составляющих.

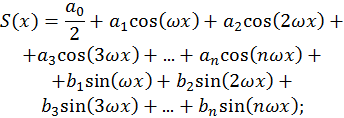
Свойства симметрии.

1. Симметрия первого рода. Если f(x) – чётная, т.е. f(-x)=f(x), то

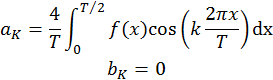
2. Симметрия первого рода. Если f(x) –нечётная, т.е. f(-x)=-f(x),

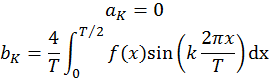
3. Симметрия третьего рода

Если f(+x)=-f(x), то

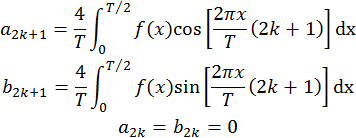
4. Симметрия 4-го рода.

а) если функция нечётн. и обладает simm 1-го рода, то a_k=b_2k=0;

б) если ф-ция чётная и обл. simm 3-го рода, то

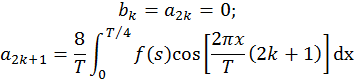
Разложим нашу функцию (simm 4-го рода, б)

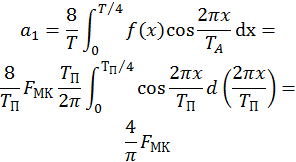
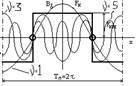
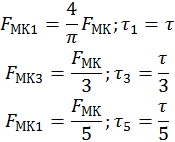
Т.к. все высшие гармоники явл. составляющими прямоугольника мдс, то они изменяются во времени (пульсируют) с одной и той же частотой, равной частоте тока в обмотке.

Найдём значение мдс первой гармоники на расстоянии x вдоль расточки статора.

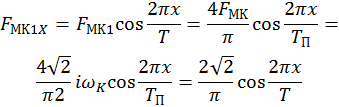
При sin-токе мдс в любой точке на статоре изменяется синусоидально во времени с амплитудою, равной F_MK1X.

Т.е. значение мдс первой гармоники в любой момент

Уравнение пульсирующих и бегущих волн

В э.м. могут создаваться как вращающиеся магн. поля, так и поля, неподвижные в пр-ве, но пульсирующие во времени. Математическое выражение волны, пульсирующей во времени по sin-закону, и распред. в пр-ве по sin-закону, может быть представлено в таком виде:

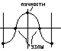
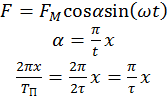В узлах в любой момент t, мдс=0, в пучностях – мдс=max.

Пульсирующую волну можно разложить на 2 составляющие.

Докажем, что пульсирующую волну можно разложить на две встречно бегущих волны мдс.

1. wt=0

Правобегущая волна мдс:

2. wt=p/2

Левобегущая волна мдс:

Пульсирующую волну мдс можно разложить на две одинаковые встречно бегущие волны мдс.

На статоре асинхронной машины уложена 3ф-обмотка, каждая из фаз к-рой сдвинута в пр-ве на 120 эл/градусов. В катушках фаз протекают токи, к-рые сдвинуты во времени на 120 эл/град. Докажем, что три пульсирующих поля, сдвинуты в пр-ве и времени на 120 эл/град., образуют вращающееся магнитное поле.

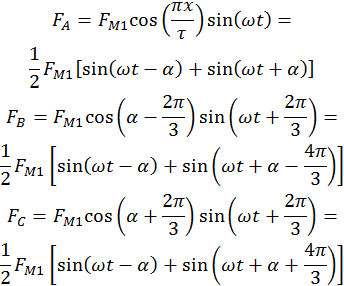
Суммируем для получения окончательного уравнения. В результате, получим:

Задача. Доказать, что два пульсирующих поля, сдвинутых в пр-ве и времени относительно друг друга на p/2 так же образуют синусоидальное вращающееся поле.

МДС 3ф-обмоток

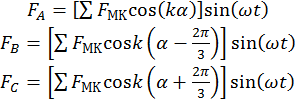В результате, мдс каждой гармонич. сост. может быть получена сложением гармоник всех 3х фаз.

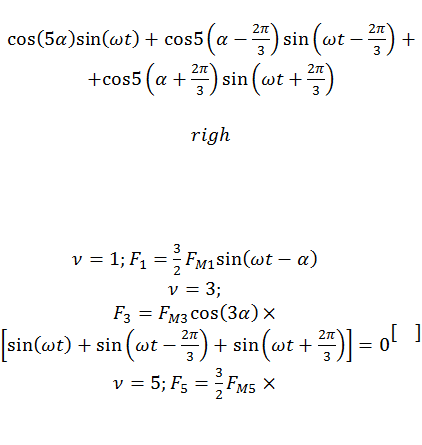Общее выражение для n-той гармоники

n=6k-1, k=0,1,2… движутся влево, против вращения основной волны.

n=6k+1, k=0,1,2… движутся вправо, по направлению вращения основной волны.

Все гармонические мдс создаются синусоидально изменяющимся током основной частоты. С другой стороны, пространственная гармоническая n-го порядка имеет по сравнению с основной гармонической в n раз меньший пространственный период, следовательно, в n раз больше число пар полюсов p. Следовательно, скорость вращения n-той гармонической относительно обмотки, будет в n раз меньше по сравнению с первой обмоткой.