области больших скольжении интенсивность увеличения тока I /2 c ростом скольжения уменьшается, и момент двигателя уменьшается примерно по тому же закону, что и cosψ2. Макс. момент наступает при критическом скольжении SK.
Чтобы найти знач-я SK и МK, продифференцируем выражение для эл.маг-го момента по S и = 0.
dM/dS = d/dS{(m1U12 ∙ r2′ ∙ S)/ω1[(r1S + r2′)2 + S2(x1 + x2′)2]} =
=[m1U12 ∙ r2′/ ω1]∙[(r1S + r2′)2 + S2(x1 + x2′)2 –S[2r1(r1S + r2′) + 2S(x1 + x2′)]/[(r1S + r2′)2 + S2(x1 + x2′)2]2 =
= [m1U12 ∙ r2′/ ω1] ∙[r2′2 – r12S2 – S2(x1 + x2′2)2/[(r1S + r2′)2 + S2(x1 + x2′)2]2]
Анализ получ-го выражения показ-ет, что оно обр-ся в нуль, если r /22 – r 21 S2 - S2 (x1 + x /2)2 = 0
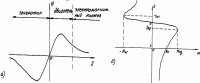Рис.1. Мех. хар-ки ас.машины а - зависимость M=f(S), б - зависимость S=f(M)
или r /22 = S2 [r 21 + (x1 + x /2)2].
Тогда критическое скольжение SK, при котором момент ас.машины имеет макс. значение, равно
Sk = ± r2′ / √[r12 + (x1 + x2′)2] = ± r2′ / √[r12 + xk2 ]
Результирующий эл.маг. момент найдем путем интегр-ия элементарного по x где xK=x1+x2’;
знак (+) соответствует работе асинхронной машины в качестве двигателя, знак (-) - в качестве генератора. Подставляя положительное значение SK в выражение для эл.маг-го момента, получим выражение для критического момента в двигательном режиме
Mкд = [m1U12/ ω1] ∙ [ (r2′√[r12 + xk2])/r2′(r1 + r2′ ∙ {√[r12 + xk2]/r2′})2 + xk2 =
= [m1U12/ ω1] ∙ [ √[r12 + xk2]/(r1 + {√[r12 + xk2]/r2′})2 + xk2
Раскроем круглые скобки в знаменателе полученного выражения и разделим числитель и знаменатель на √[r12 + xk2] получим Mкд = [m1U12/ 2ω1(√[r12 + xk2] + r1)]
Подставляя отриц. значение SK в выражение для эл.маг-го момента, получим аналогичное выраж-е для критич. момента ас.машины в гене-ом режиме Mкг = - [m1U12/ 2ω1(√[r12 + xk2] - r1)]
Найдем отношение критических моментов ас.машины в генер-ом и двиг-ом режимах
Mкг/ Mкд = (√[r12 + xk2] + r1)/ (√[r12 + xk2] - r1) = -(1 – ε)/( 1 + ε); ε = r1 / √[r12 + xk2] = Sk(r1/r2′)
Таким образом, значение критич. момента в генер-ом режиме больше, чем в двиг-ом, что обусловлено влиянием падения напряжения на активном сопротивлении обмотки статора.
В практических расчетах удобно выражать электромагнитный момент M в долях от максимального момента Mкд ; M/Mкд = [{2r2′S(√[r12 + xk2] + r1)}/( r1S + r2′)2 + S2xk2]
В полученном выражении числитель и знаменатель разделим на r2′S√[r12 + xk2]
M/Mкд = 2(1 + ε)/[(S/Sk) + (Sk/S) + 2ε], Если принять r1=0, тогда ε=0, формула упр-тся и примет вид M = 2Mкд /[(S/Sk) + (Sk/S)]
Это выражение известно в технической литературе как формула Клосса. Задаваясь значениями скольжения S, можно построить мех. хар-ку ад.
Одним из важнейших эксплуатационных параметров ад является кратность макс-го момента или перегрузочная способность двигателя λМ, которая равна отношению крит-го момента к ном-му при ном-ом напряжении λМ=МКД/МНОМ
47.Влияние изменения напряжения источника питания на мех. хар-ки ас. машины
Для изменения U, подводимого к статорной обмотке ас.машины, прим-ся регул-е источ-и напряжения, например, автотра-ор, индукционный регулятор, тиристорный регул-р Uя и др.
Пусть частота U, подводимого к обмотке статора, остается неизменной f1=const. Как влияет изменение напряжения ист-а питания на мех. хар-ки ас машины?
В пределах рабочего участка мех-ой хар-ки (-SK<S<SK), когда ток статора не превышает существенно ном-го значения, ЭДС двигателя Е1 незначительно отличается от напряжения сети U1, поэтому можно приближенно записать U1≈E1=4,44f1w1Фm.
Из формулы следует, что
при условии f=const изменение U приводит к соответствующему
изменению маг. потока ас. машины. Так как в ном-ом режиме маг-я цепь
двигателя насыщена рис.1, то подача на обмотку статора U выше
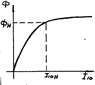ном-го приводит к знач-му
увеличении тока намаг-ия I10. У двигателей общепромышленного
назначения ток холостого хода составляет I10=(0,25..0,35)I1НОМ, поэтому повышение напряжения на 20..30% может
увеличить ток хх до значений, превышающих номинальный ток I1НОМ и двигатель может нагреться
этим током сверх допустимой температуры даже при отсутствии полезной нагрузки
на его валу. Поэтому в дальнейшем будет рассматриваться влияние на
механические характеристики асинхронной машины только изменения напряжения от
номинального значения до нуля. Итак, пусть напряжение U1, подаваемое на статорную обмотку
ад, ↓ от ном-го значения. Угловая скорость вращения маг-го поля не зависит от
U ω1=2πf/p, →, все мех. хар-ки пройдут
через одну точку на оси ординат, соответствующую режиму идеального хх ад (S=О). Момент, развиваемый
двигателем при любом скольжении, пропорционален квадрату приложенного
напряжения , а токи обмоток статора и ротора пропорциональны приложенному
напряжению; I2′ = U1/√[(r1 + (r2′/S))2 + xk2]; I1=U1[1/Zm+ 1/(Z1+Z /2S)].
Рис.. Механические
характеристики ад при изменении U источника питания.
Из приведенного на рис. семейства мех. хар-ик ас.маш. при изменении U видно, что критическое скольжение для всех хар-ик const, и не зав-ит от U: Sk = ± r2′/√[r12 +xk2]
Крутизна характеристик при ↓ U ↑, но так как Sк остается const, то регулирование скорости двигателя возможно лишь в узких пределах. Коэфф. мощности при ↓ U имеет тенденцию к ↑, особенно заметному
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.
