


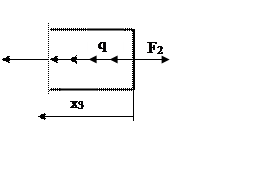
Задача решается методом сечения, который применяется отдельно для каждого участка балки. Будем двигаться справа налево, т.е. сначала отбрасываем часть стержня большего сечения, содержащую жесткую заделку (участок №3).
1. Находим величину продольного усилия, действующего на сечение:
|
![]() ,
, ![]()
![]()
![]()
![]()
2. Находим величины нормальных напряжений:
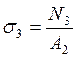
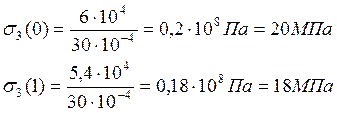
3. Находим величину абсолютного удлинения:
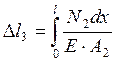
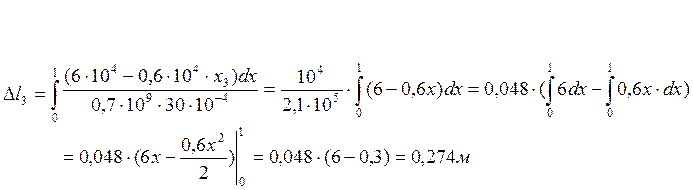
Теперь рассмотрим сечение, проходящее через левую часть стержня, но не включающее действие силы F1 (участок №2).
1. Находим величину продольного усилия:
![]()
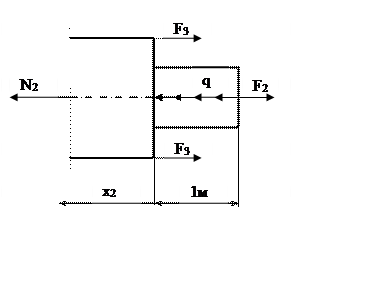
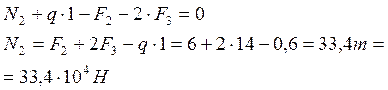
2. Находим величину нормального напряжения, возникающего в сечении:
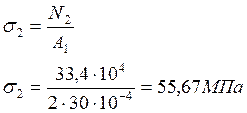
3. Определяем величину абсолютного удлинения:
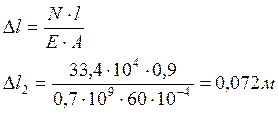
Рассмотрим последнее сечение, включающее в себя все внешние силы, действующие на стержень (участок №1).
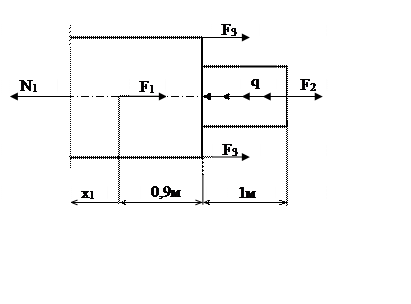 1.
Рассчитываем величину продольного усилия:
1.
Рассчитываем величину продольного усилия:
![]()
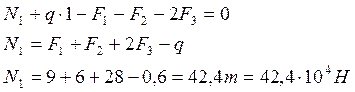
2. Определяем величину нормального напряжения:
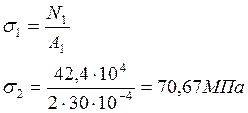
3. Определяем величину абсолютного удлинения:
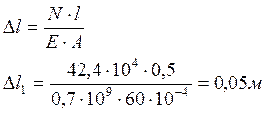
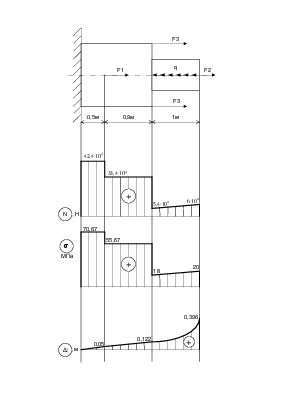
Найдя все необходимые данные, приступаем к построению эпюр. Эпюра абсолютных удлинений начинает строится от жесткой заделки, где Δl=0. На третьем участке, где действует сила q, эпюра абсолютных удлинений будет иметь вид параболы.
Чтобы построить эпюру абсолютных удлинений, применяют метод последовательного суммирования, т.е.:
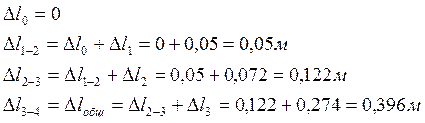
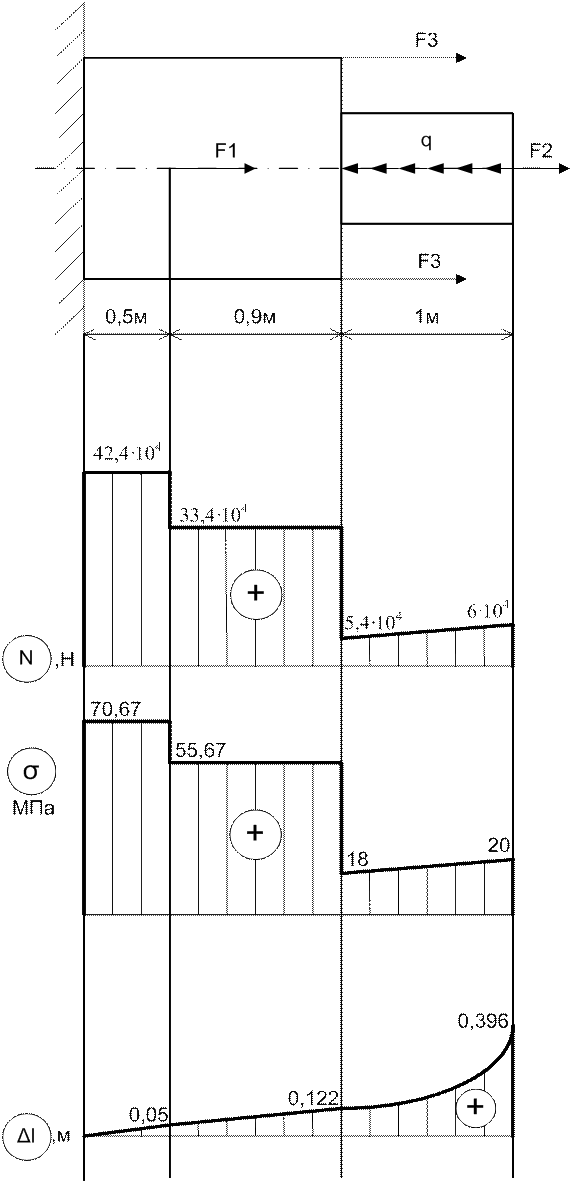
Проанализировав полученные эпюры, можно сделать следующие выводы:
1. Из анализа эпюры продольных усилий, видно, что реакция в жесткой заделке равна 42,4 т. Также видно, что на всех участках происходит растяжение стержня, т.к. на всех участках N>0.
2. Рассматривая эпюру нормальных напряжений, можно увидеть, что опасным сечением являются все сечения первого участка, т.к. /σмак/=/σ1/=70,67 МПа.
3. Анализируя эпюру абсолютных удлинений, видно, что правый торец стержня будет смещаться вправо под действием данных сил на 0,396 м, т.к. Δlобщ=0,396м>0.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.