







ГОУ ВПО НТИ УГТУ УПИ
кафедра математики
Расчетно-графическая работа
по теоретической механике
С3, Д2, Д3
Вариант: 12
Группа: 2414 – ЭАПУ
Студент:
Преподаватель:
г.Н.Тагил
Задача К1
Дано:
Закон движения точки 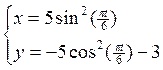
t1=1
Найти:
x=f(y); ut=1=?; at=1=?; pt=1=?
Решение:
1) Находим траекторию:
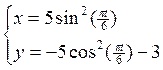
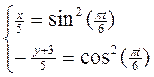
sin2a+cos2a=1 => ![]()
x – y – 3 = 5
x = 8 + y, т.е. траекторией точки является прямая
2) Находим координаты точки и строим ее:
![]()
![]()
3) Находим скорость точки через ее проекции на оси координат:
![]()
![]()
![]()
![]()
![]()
4) Находим ускорение точки через ее проекции на оси координат:
![]()
![]()
![]()
![]()
![]()
|
Координаты, см |
Скорость, см/с |
Ускорение, см/с2 |
Радиус кривизны |
|||||||
|
х |
y |
ux |
uy |
u |
ax |
ay |
a |
at |
an |
r |
|
1.25 |
-6.75 |
2.266 |
2.266 |
3.205 |
1.369 |
1.369 |
1.936 |
1.936 |
0 |
- |
Задача К2
Дано:
R2=20; r2=15; R3=10; x0=5; u0=10; x2=179; t1=2; t2=3
Найти:
aм=?; uм=?; w3=?; e3=?
Решение:
Уравнение движения груза 1 имеет вид: х = c2t2+c1t+c0.
При t = 0 х0=5см, ![]() =10см/с, при t2=3c х2=179см
=10см/с, при t2=3c х2=179см
Скорость груза 1: ![]() .
.
Подставляя в формулы данные получим коэффициенты: с0=5; с1=10; с2=16.
Таким образом, уравнение движения груза 1 имеет вид: x = 16t2 + 10t + 5.
Скорость груза 1: ![]() .
.
Ускорение груза 1: ![]()
В соответствии со схемой механизма составим уравнения:
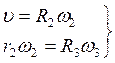 откуда
откуда 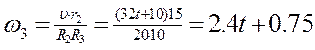
Угловое ускорение колеса 3: ![]()
Скорость точки М, ее вращательное, центростремительное и полное ускорения определяются по формулам:
uм=R3w3=10×5.55=55.5;
![]() ;
;
![]() ;
;
![]()
|
u, см/с |
a, см/с2 |
w3, рад/с |
e3, рад/с2 |
uм, см/с |
см/с2 |
см/с2 |
ам, см/с2 |
|
74 |
32 |
5,55 |
2,4 |
55,5 |
57,6 |
24 |
62,4 |
Задача К3
Дано:
АВ=30; АС=20; uА=20; аА=20.
Найти:
uВ=?; uС=?; аВ=?; аС=?; w=?; e=?.
Решение:
Находим мгновенный центр скоростей: uВ=0 следовательно точка В – мгновенный центр скоростей звена АВ. От сюда следует:
![]() ;
;
uс= wАВ×ВС=wАВ(АВ – АС)=6,67см/с.
Определение ускорения точки и углового ускорения звена:
![]() ;
;
![]()
![]() ;
; ![]() ;
;
![]() ;
; ![]() .
От сюда следует:
.
От сюда следует: ![]()
Определяем ускорение точки С:
![]() ;
;
![]() ;
;
![]()
![]()
Задача С3
Дано:
Р1=12.0кН; Р2=4.0кН; М=16.0кН×м; q=3.0кН/м.
Найти:
RВ=?
Решение:
Рис.1
Рассмотрим правую часть конструкции (рис.2):
åхi =0 ; xc – P2 = 0;
åyi =0; RD – yc = 0;
åMDi =0; -xc×3+P2×2 – M + yc ×3= 0;
xc
= P2 = 4.0кМ; RD
= yc; ![]() ; RD=6.67
кН.
; RD=6.67
кН.
Рассмотрим левую часть конструкции (рис.3):
åxi =0; q×4– P1cosa – x¢c – xB = 0;
åyi =0; RA – P1sina + y¢c – yB = 0;
åMB=0; – RA×4 – q×4×2 + P1cosa×4 + P1sina×2 + x¢c×3 =0
xB = q×4 – P1cosa - x¢c = 2кН;
![]()
yB= RA – P1sina+ y¢c=4.4кН;
![]()
Рассмотрим кривую часть конструкции (рис.4):
åхi =0 ; xc – P2 = 0;
åyi =0; RD = 0;
åMDi =0; Мс – М + Р2×2 – хс×3 = 0;
хс= Р2 = 4кН; Мс= М + хс×3 – Р2×2=20кН.
Для левой части конструкции (рис.5):
åxi =0; q×4 – P1cosa – x¢c – xB=0;
åyi =0; RA – P1sina + yB=0;
åMBi=0; – 4×q×2 + P1cosa×4 + P1sina×2 + x¢c×3 – RA×4 – M¢c=0;
xB=q×4 – P1cosa – x¢c;
![]()
yB=P1sin×a – RA=7.2кН;
![]()
Модуль реакции RB увеличился в 1.56 раза.
Задача Д2
Дано:
m; ![]() ; z0=R;
; z0=R; ![]() ; 0<R=const.
; 0<R=const.
Найти:
Уравнение движения тела М массой m.
Решение:
![]() ;
; ![]() ;
;
![]() (1)
(1)
Пусть ![]() ;
; ![]() ;
;
Подставляем в уровнение (1) получим: ![]()
Разделим переменные: ydy= – gR2z-2dz (2)
Проинтегрировав уравнение (2) получим: ![]() ;
или
;
или
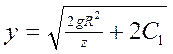 ;
; 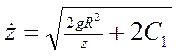 ,
где С1 – постоянная интегрирования
,
где С1 – постоянная интегрирования
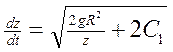 (3)
(3)
Найдем С1 из условий: z0=R; ![]() , тогда:
, тогда:
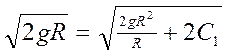 из этого уравнения следует,
что С1=0;
из этого уравнения следует,
что С1=0;
тогда уравнение (3) будет выглядеть так: 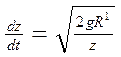 или
или
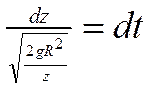
Проинтегрируем обе части уравнения: 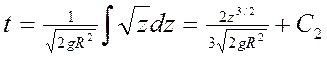 .
.
При t=0; z0=R, тогда: 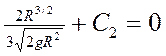 ;
;
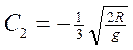 ;
; 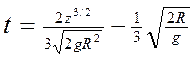
или ![]() отсюда:
отсюда:
![]()
Задача Д3
Дано:
m=3кг; l=2см; с=9Н/см=900Н/м; x=1,2sin8t.
Исследовать колебательное движение материальной точки.
Решение:
![]() ;
; ![]() ;
Р=с(х-x);
;
Р=с(х-x); ![]() = –сх + сx ;
= –сх + сx ; ![]() , подставим числовые значения:
, подставим числовые значения: ![]() (1)
(1)
![]() ; k2+300=0;
; k2+300=0; ![]() ;
; ![]()
х2= В1sin8t+B2cos8t; ![]() .
.
Подставляем полученные значения в уравнение (1):
-64B1sin8t – 64B2cos8t + 300B1sin8t+300B2cos8t=3,6sin8t. Отсюда: 236В1=3,6; 236В2=0; В1=0,015; В2=0.
И тогда х2=0,015sin8t; ![]()
![]() .
.
Постоянные С1 и С2 найдем из начальных условий:
при t=0; x0= – l; ![]() ;
;
![]() ; C1= – 0,02;
C2= –0,07. Отсюда:
; C1= – 0,02;
C2= –0,07. Отсюда:
![]()
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.