Структурные матричные схемы и передаточные матрицы. Математические модели в пространстве состояний. Синтез многомерных систем

Взаимосвязь двух видов представления многомерных систем управления существует, и более того в пункте 5 настоящего курсового проекта проведена с достаточной точностью;

2  Следует отметить применимость обоих представлений к анализу и синтезу систем управления;

3  Расчеты, проведенные в данном пункте верны.

Стоит отметить также, что графики, полученные в системах в виде математических моделей получить проще, но стоит делать поспешных выводов, т.к. двухконтурная система подчиненного регулирования двигателем постоянного тока проста, а применение структурно-матричного представления облегчает синтез более сложных многомерных систем регулирования.

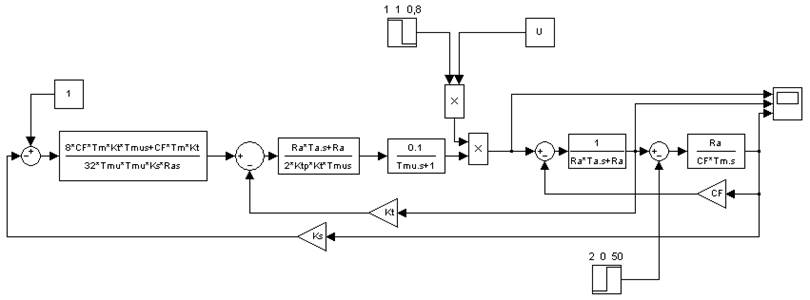
Рассмотрим переходные процессы при падении напряжения сети до 0,8 от номинального в момент времени – 1 с. И набросе нагрузки в момент времени – 2 с.

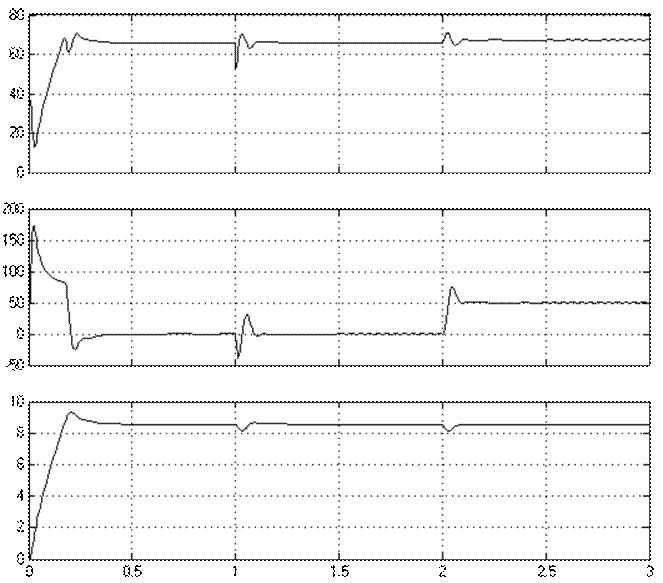
Рисунок 7.15 Осциллограмма подводимого напряжения к двигателю,

 нагрузочная диаграмма и тахограмма двигателя

Вывод: мы видим, что система астатическая как по отношению к сигналу задания, так и к сигналу возмущения, и по окончании переходного процесса происходит восстановление скорости на заданном уровне.

Заключение

В данном проекте были рассмотрены теоретические основы многомерных систем электропривода, а также их практическое применение и способы расчета и моделирования в программах MathCad и MatLab.

Библиографический список

1  Крутько П.Д., Алгоритмы и программы проектирования автоматических систем. – М:1988, 306с.

2  Дезоер Ч., Видъясагар М., Системы с обратной связью: вход-выхлдные соотношения. – М: Наука, 1983, 380с.

3  Ивановский Р.И., Таранов А.Г. Синтез МСАУ с применением ЦВМ. – М., Наука, 172с.

4  Ивановский Р.И. Компьютерные технологии в науке и образовании. Практика применения систем MathCAD Pro. – М.: Высшая школа. 2003. – 432с.

Приложение

Применение интегрированного пакета MATLAB 6.5/Simulink для расчета многомерных систем.

Как уже говорилось выше, основным минусом применения многомерных систем является сложность их расчета, высокий порядок получаемых дифференциальных уравнений. Поэтому расчет вручную весьма затруднен, примером может стать вариант разбора системы подчиненного регулирования рассмотренный выше, или даже пример, на первый взгляд простой, разбора двигателя постоянного тока.

В настоящий момент, в современных условиях имеется достаточное множество программных средств, позволяющих осуществлять сложные функциональные преобразования и аналитические выкладки на компьютерах. Подобными возможностями обладают такие системы компьютерной математики, как Maple, Mathematica, MathCAD, MATLAB, а также многие другие программы. Отличительной особенностью программы MATLAB является встроенное приложение Simulink, которое позволяет моделировать любые системы, любой сложности, снимать временные характеристики, а также содержит встроенные блоки определения передаточных функций по системе вход-выход, определять элементы параметрических матриц А, В, С, D. Стоит отметить применимость данных функций программы к многомерным системам.

В качестве первого примера возьмем рассмотренный выше электродвигатель постоянного тока. Напомним, что в итоге преобразований мы получили передаточную матрицу

.

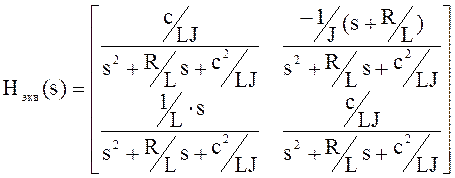Что соответствует передаточным функциям объекта

.

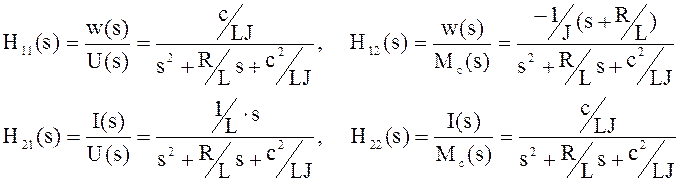С помощью перекрестных связей представим полученные матрицы в MATLAB 6.5/Simulink и проверим верность полученных выражений.

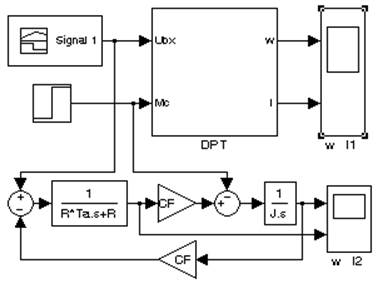
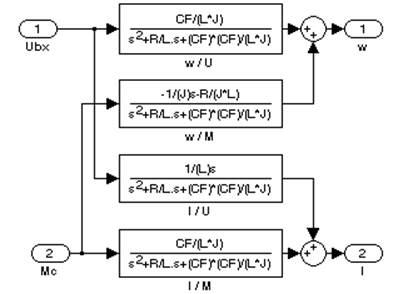
Рисунок П1 Представление двигателя в программе MATLAB 6.5/Simulink: а-математическая модель ДПТ, представленная в качестве матричных таблиц и структурной схемой; б-подсистема DPT.

При этом наброс нагрузки происходит на пятой секунде, а временная характеристика входного напряжения имеет вид

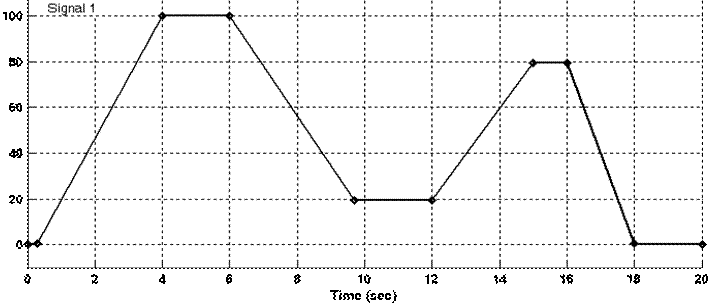
Рисунок П2 Осциллограмма входного напряжения

Запустим схему и получим идентичные результаты

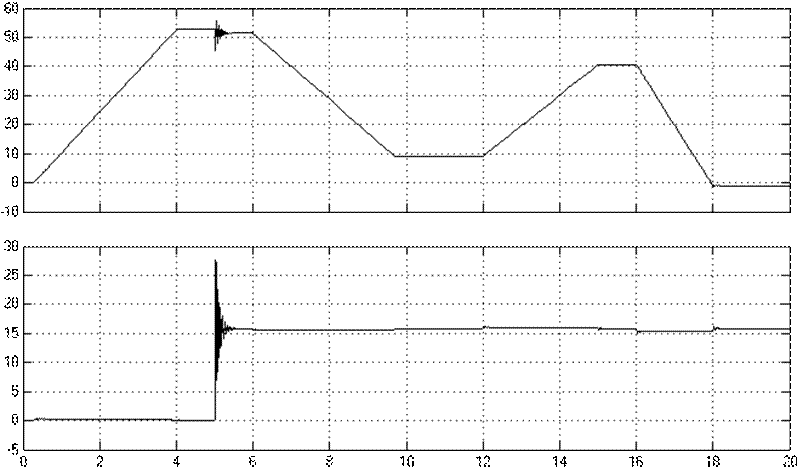
Вывод: одинаковые результаты моделирования свидетельствует о верности произведенных выше расчетов.

Также с помощью MATLAB 6.5 можно получить передаточную функцию, для этого необходимо:

1 Представить математическую модель в виде системы вход-выход, т.е. входом будет та входная величина, относительно которой будет изменяться нужный выход;

2 В окне команд или в М-Файле написать программу, указав необходимые параметры схемы и коэффициенты:

[A,B,C,D] = linmod (‘указывается имя сохраненного файла со схемой’);

[num,den] = ss2tf (A,B,C,D);

W = tf(num, den)

3 Запустить программу и в окне команд высветится

Transfer function:

-3.553e-015 s + 6072

---------------------------------------------------------------------------------------s^2 + 19.63 s + 1.152e004

Стоит заметить, что одновременно с определением передаточной функции происходит определение параметрических матриц A, B, C, D, значение элементов которых можно увидеть над передаточной функцией в окне команд, например

A = 0   243.3611

-47.3320   -19.6280.

Единственным минусом, которым обладает данный способ расчета передаточных функций, это невозможность получения передаточных функций в символьном виде (в общем виде), т.е. расчет производится для определенного, с заранее известными параметрами, двигателя, что чаще всего и требуется на практике.

В качестве второго примера рассмотрим двухконтурную систему подчиненного регулирования двигателем постоянного тока независимого возбуждения. В данном случае мы имеем три входа (U_зад.(t), U_пит.(t), I_c(t)) и два выхода (w(t), I(t)) – система многомерна. Определим элементы передаточной матрицы указанным выше способом.

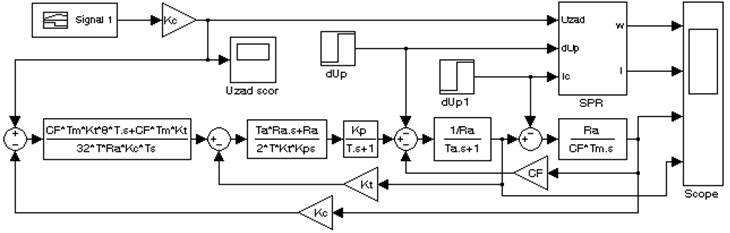
Рисунок П4 Передаточная матрица и структурная схема системы