Определение потерь теплоты через поверхность стенки. Измерение температуры. Определение физических свойств

Задача 3.3.

Задание: определит потери теплоты через поверхность стенки, показанной на рисунке 1, если известны температуры воздуха с внутренней стороны стенки , и наружной - , . С наружной стороны стенка омывается воздухом со скоростью . Стенку считать однослойной, выполненной из силикатного кирпича, с коэффициентом теплопроводности 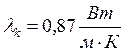. В стенке имеются три оконных проёма с двойными рамами, толщина стекла в которых , а расстояние между внутренними поверхностями стёкол 1. Коэффициент теплопроводности стекла 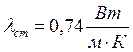. Исходные данные приняты из таблицы 3.3. Построить в масштабе графики изменения температур в процессе теплообмена через оба участка стены.

,	14
,	-30
,	150
,	15
,	3
,	0,74
,	0,87

Решение:

I    Потери тепла через стенку.

1  Задаемся изменением температуры

Определяем температуру стенки , ,

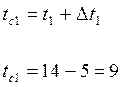
Определяем физические свойства при  ,

=0,7052

Определим  β

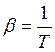
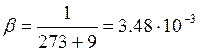
Определяем высоту ,H, м

Н=2,81

Находим число Гразгофа

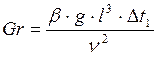
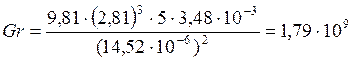
Определяем соотношение:

  - 2 участка

Ламинарный пограничный слой

Определяем границу между сечением ,м

  

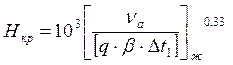
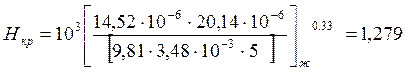
 при

Находим число Гразгофа

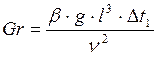
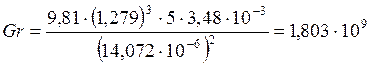
Из известных данных находим число Нуссельта для ламинарного слоя.

Тарбулентный пограничный слой

Определяем высоту

Находим число Гразгофа

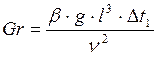
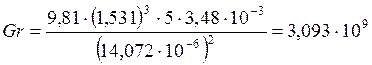
При =14

 

Из известных данных находим число Нуссельта для тарбулентного слоя

Определяем средний

Первый участок:

Тепловые потери определяются для двух участков раздельно стена (кирпичная кладка) – как однослойная плоская стенка. Температурные напоры, коэффициенты теплопередачи , , плотность теплового потока находятся графоаналитическим методом последовательных приближений. Омывание внутренней стороны стенки рассматривается как свободная конвекция в большом объёме. При значении  устанавливается ламинарный режим и для вертикальной пластины коэффициент теплоотдачи  может быть найден по формуле,

(1).

В этой формуле определяющий размер – высота стенки . Определяющая температура – температура воздуха вдали от стенки. Значение  определяется при температуре стенки. Поскольку температура стенки неизвестна, то для однослойной плоской стенки необходимо задаться рядом значений , например 5, 12.

При значениях  на вертикальной стенке образуются два участка – ламинарный пограничный слой, а за ним турбулентный. Границей между ними служит сечение на высоте , значение которой определяется по формуле

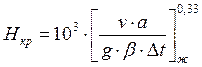(2).

В формуле (1)  - число Гросгофа

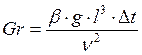 (3),

где  - коэффициент объёмного расширения среды, для газа ;

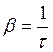 - коэффициент кинематической вязкости, ;

- ускорение силы тяжести, , ;

 - длина, то есть высота , ;

 - число Прандтля, определяющее физические свойства жидкости.

При  имеем

 ()

 ()

Следовательно,

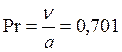
, следовательно, на вертикальной стенке образуются два участка – ламинарный пограничный слой, а за ним турбулентный. Границей между ними служит сечение на высоте , значение которой определяется по формуле (2),

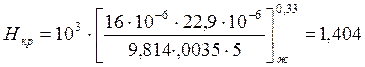
Найдем высоту теплоотдачи на турбулентном участке ,

Рассмотрим ламинарный режим:

Найдём коэффициент Прандтля для данного режима

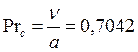
Найдём число Гросгофа для данного режима по формуле (3)

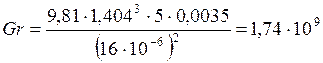
В этом случае теплоотдача на ламинарном участке до высоты  определяется по формуле (1), а на турбулентном высотой  по формуле

(4)

По формуле (1)

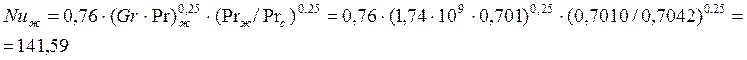
Рассмотрим турбулентный режим:

Найдём число Гросгофа для данного режима по формуле (3)

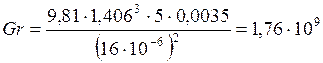
Найдем число Нюссельта для данного режима по формуле (4),

Так как число Нюссельта определяется по формуле

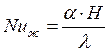 (5),

то 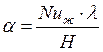 (6), где

Найдём средние коэффициенты теплоотдачи на ламинарном и турбулентном пограничных слоях,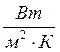

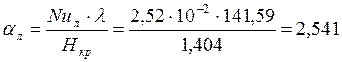
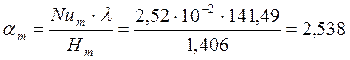
Средний коэффициент теплоотдачи,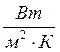

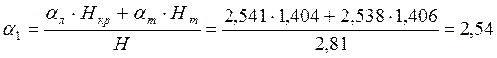
Плотность теплового потока определяется по формуле Ньютона,

          Температура наружной поверхности стенки находиться по уравнению Фурье,

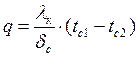
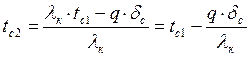
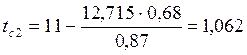
Коэффициент теплоотдачи  с наружной стороны стенки может быть определён для случая продольного обтекания пластины. При этом для ламинарного режима

Для турбулентного режима

,

где  - число Рейнольдса

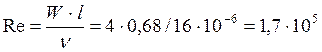
Найдём коэффициент Прандтля для данного режима

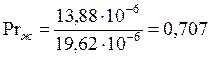
Находим коэффициент теплоотдачи ,

,

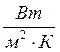
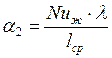где  - средняя длина стены, которая находиться по формуле,

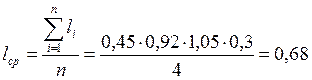
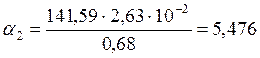
Определяем температурный напор,

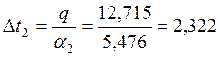
Второй участок:

При  имеем

Число Прандтля

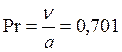
Найдём число Гросгофа по формуле (3)

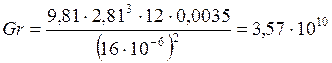
 - поток турбулентный

Найдём высоту  по формуле (2), 

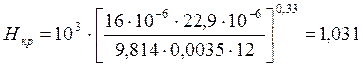
Найдем высоту теплоотдачи ,

Рассмотрим ламинарный режим:

Число Прандтля

Найдём число Гросгофа по формуле (3)

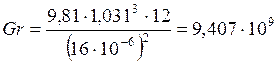
По формуле (1)

Рассмотрим турбулентный режим:

Найдём число Гросгофа по формуле (3)

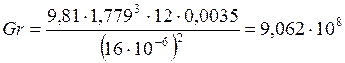
Найдем число Нюссельта для данного режима по формуле (4),

Так как число Нюссельта определяется по формуле

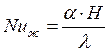 (5),

то 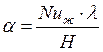 (6), где

Найдём средние коэффициенты теплоотдачи на ламинарном и турбулентном пограничных слоях,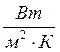

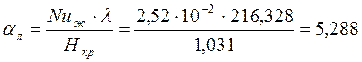
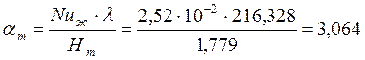
Средний коэффициент теплоотдачи,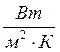

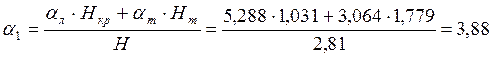
Плотность теплового потока определяется по формуле Ньютона,

()

Определим температурный напор

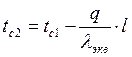
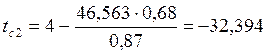
Найдём число Рейнольдса

Найдем число Нюссельта для данного режима по формуле ,

Находим коэффициент теплоотдачи ,

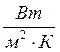
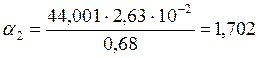
Температурный напор

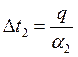
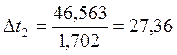
Из уравнения теплового потока выразим ,

Найдём общие числовые потери через стенку по формуле,

,

где ,  - плотность теплового потока и площадь поверхности на первом и втором участке стены.