Растровая развертка сплошных областей. Заполнение многоугольников. Простой алгоритм закраски с упорядоченным списком ребер

Закраска

(Растровая развертка сплошных областей)

• Генерация сплошных областей из простых описаний ребер или вершин многоугольника называется растровой разверткой сплошных областей, заполнением многоугольников или заполнением контуров.
• Два подхода:
• Растровая развертка
• Затравочное заполнение
• В методах растровой развертки в порядке сканирования строк пытаются определить, лежит ли точка внутри многоугольника или контура. При этом идут от верха многоугольника или контура вниз.

В методах затравочного заполнения предполагается, что известна некоторая точка (затравка) внутри замкнутого контура. В алгоритмах ищут точки, соседние с затравкой и расположенные внутри контура. Если соседние точки расположены не внутри, значит обнаружена граница контура. Если точка оказалась внутри контура, то она становится новой затравочной точкой и поиск продолжается рекурсивно.

Заполнение многоугольников

Простейший метод – проверка на принадлежность внутренности МУ каждого пикселя в растре. Это расточительно, так как обычно большинство пикселей лежит вне МУ. Вычисляем для МУ прямоугольную оболочку – наименьшей прямоугольник, содержащий внутри себя многоугольник.

Достаточно эффективно

Не очень эффективно

Более эффективный метод использует тот факт, что соседние пиксели имеют одинаковые характеристики (кроме пикселей граничных ребер), так называемая «пространственная когерентность». Для растрового графического терминала соседние пиксели на одной сканирующей строке, вероятно, имеют одинаковые характеристики. Это когерентность растровых строк. Характеристики пикселей на данной строке изменяются только там, где ребро МУ пересекают строку. Эти пересечения делят сканирующую строку на области.

8

P5

P3

6

4

P4

Сканирующая строка 4

Сканирующая строка 2

2

P1

P2

0

2

4

6

8

10

Сканирующая строка 2: x < 1 – вне МУ; 1  x  8 – внутри МУ; x > 8 – вне МУ

Сканирующая строка 4 делится на пять областей: x < 1 – вне МУ; 1  x  4 – внутри МУ; 4 < x < 6 – вне МУ; 6  x  8 – внутри МУ; x > 8 – вне МУ

Необязательно, чтобы точки пересечения для строки 4 сразу определялись в фиксированном порядке (слева направо). Например, при задании МУ списком вершин P1P2P3P4P5P1 или списком ребер – последовательными парами вершин P1P2, P2P3, P3P4, P4P5, P5P1 – для строки 4 точки пересечения с ребрами МУ: 8, 6, 4, 1. Эти точки надо отсортировать в возрастающем порядке по x: 1, 4, 6, 8.

Для определения цвета пикселей на сканирующей строке рассматриваются пары отсортированных точек пересечений. Для каждого интервала, задаваемого парой пересечений, используется цвет заполняемого МУ. Для интервалов между парами пересечений и крайних (от начала строки до первой точки пересечения и от последней точки пересечения до конца строки) используется фоновый цвет. Таким образом, для строки 4 в фоновый цвет устанавливаются пиксели: от 0 до 1, от 4 до 6, от 8 до 10, а пиксели от 1 до 4 и от 6 до 8 окрашены в цвет МУ.

Точное определение пикселей, которые должны закрашиваться в цвет МУ, требует некоторой осторожности.

6

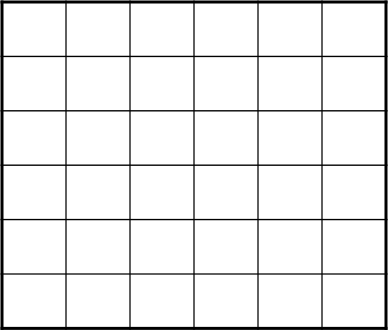
Пересечение сканирующих строк с 1 до 4 с ребрами ПУ: x = 1 и x = 5. Пиксели адресуются координатами своего левого нижнего угла, значит для каждой

5

4

3

2

1

0

2

4

6

1

3

5

из этих сканирующих строк будут закрашиваться пиксели с x – координатами 1, 2, 3, 4 и 5.

5

4

3

2

1

0

2

4

6

1

3

5

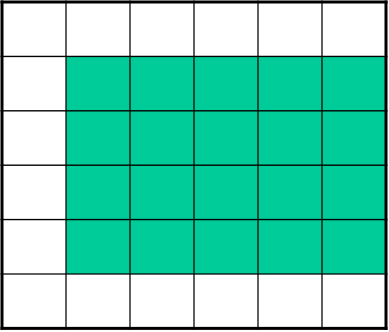
Результат: закрашиваются пиксели вне ПУ. Модифицируем систему координат сканирующей строки и тесты закраски пикселей.

Примем: сканирующие строки проходят через центр строк пикселей, т. е. через середину интервала.

6

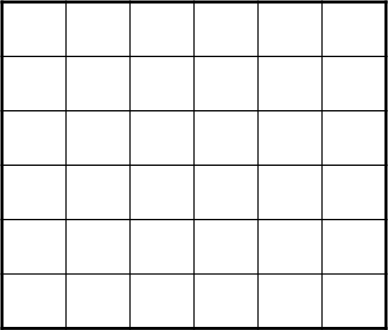
сканирующая строка

5

4

3,5

3

2,5

2

1,5

1

0

2

4

6

1

3

5

Закрашиваются пиксели, центры которых расположены справа от пересечения внутри интервала.

Результат закраски:

6

5

4

3,5

3

2,5

2

1,5

1

0

2

4

6

1

3

5

Горизонтальные ребра на пересекают сканирующие строки и поэтому игнорируются.

Простой алгоритм закраски с упорядоченным списком ребер

Определить для каждого ребра МУ точки пересечений со сканирующими