Информатика и выч. техника \ Вычислительные машины, системы и сети

Программная модель процессора IntelPentium (IA-32). Программная модель – Регистры. Прикладная модель CPU, страница 3

Регистр тегов

TW – Tag Word

Регистр содержит 16-и разрядное слово, состоящее из 8-и (по числу регистров данных) 2х битных тегов, характеризующихся содержимым соответствующих регистров данных.

Размещение тегов в регистре соответствует физическим адресам регистра данных, а не логическим (используемых в программе на Assembler).

В связи с этим, для проверки содержимого регистра по его тегу в программе на Assembler необходимо выполнить обращение к вершине стека и преобразовать логический адрес проверяемого регистра в физический адрес его тега.

Значение тегов регистров данных.

tagi     =      00     носит наименование Valid

Регистр содержит допустимое (нормализованное) вещественное число.

01  Zero

Регистр содержит нулевые значения.

В FPU принято использовать знаковое представление «0»   (+0/-0). Модуль нуля представляется кодом полного нуля (все разряды равны нулю).

10  Special

Регистр содержит специальные значения, к которым относятся денормализованные числа, положительные и отрицательные бесконечности, нечисла (NaN – Not a Number), неопределенность и неподдерживаемые форматы.

11  Empty (пустой регистр)

Попытка использования пустого регистра в качестве операнда приводит к особому случаю недействительной операции: IE – Invalid operation Error.

Представление чисел различных типов на числовой оси

Представление крайних значений нормализованных чисел в форматах ОТ/ДТ:

          x |11 … 10| |11 … 11|          3,37·1038 / 1,67·10308

          x |00 … 01| |00 … 00|          1,17·10-38 / 2,23·10-308

В формате РТ:

          x |11 … 10| |11 … 11|          1,18·104932

          x |00 … 01| |1.00… 0|          3,37·10-4932

Специальные значения

Денормализованные числа появляются в операциях, результат которых настолько близок к нулю, что его нормализация приводит к особому случаю исчезновения порядка (антипереполнения).

Особенностями представления денормализованных чисел являются:

·  смещенный порядок (характеристика) имеет нулевое значение неиспользуемое для представления нормализованных чисел;

·  бит целой части мантиссы (явной или не явной) равен нулю;

Представление денормализованных чисел в форматах ОТ/ДТ:

          x |00 … 00| |11 … 11|          0,58·10-38 / 1,12·10-308

          x |00 … 00| |00 … 01|          ~10-46 / ~10-324

В формате РТ:

          x |00 … 00| |0.1… 11|          1,68·10-49

          x |00 … 00| |0.0… 01|          ~10-4952

Наличие денормализованных чисел в FPU имеет следующие особенности:

1)  По мере возможности FPU старается избежать их появления, т.е. всегда нормализует числа с плавающей точкой за исключением очень малых чисел из области антипереполнения;

2)  FPU формирует особый случай антипереполнения, позволяющий обнаруживать ситуации, в которых появляются денормализованные числа;

3)  FPU формирует особый случай денормализованного операнда DE (Denormalized operand Error), позволяющий обнаружить ситуации, в которых в качестве операндов использовались денормализованные числа;

4)  В том случае, когда денормализованное число в форматах ОТ/ДТ служит операндом источника выбираемым из памяти и особый случай DE замаскирован, его преобразование во внутренний формат РТ приводит к его нормализации.

Бесконечность кодируется специальным значением, содержащим максимально смещенный порядок, представленным всеми единицами и мантиссой равной единице:

М∞ = 1.0 … 00

В форматах ОТ/ДТ с учетом скрытого разряда скрытой части мантиссы представление бесконечности содержит нулевую мантиссу, а в формате РТ старший разряд мантиссы равен единице. Значения знаковой бесконечности формируются автоматически, как результат замаскированной реакции на особый случай переполнения или деления на ноль.

Значение бесконечности может использоваться как один или оба операнда при выполнении арифметических операций. В качестве результата допустимой операции обычно формируется бесконечность с соответствующим знаком, например:

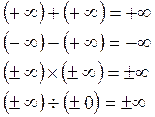
При использовании недопустимых операций с операндами бесконечностями или нулем, формируется особый случай недействительной операции IE (Invalid operation Error). К таким случаям, например, относятся:

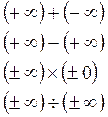
NaN (NotaNumber) представляют собой специальные значения, содержащие в формате смещенного порядка все единицы и любую мантиссу за исключением значения «1.0 … 0», используемого для представления «∞».

Скачать файл