Теория принятия решений задачи и проблемы. Задачи теории принятия решений и их место в исследовании операций

Будем считать известными данные по надежности узлов первой, второй групп и коммутаторов (p₁(t), p₂(t), p₃(t)). Требуется оценить надежность системы и определить число узлов m₁, m₂, m₃ , при котором достигается максимальная эффективность системы. Отказы компонентов системы предположим независимыми. Подключение каждого узла (сервера, накопителя) осуществляется к каждому коммутатору через отдельный сетевой адаптер, все СА идентичны и имеют надежность p_a(t). Будем предполагать, что обслуживание, включающее замену (восстановление) отказавших компонент, производится через заданное время t. В интервалах между обслуживанием происходит накопление отказов (деградация системы). Распределение времени между отказами будем считать экспоненциальным. При оценке надежности рассматриваются режим резервирования с разделением нагрузки и режим переключения резерва при реконфигурации. В режиме резервирования с разделением нагрузки через все исправные коммутаторы может поддерживаться одновременный обмен между различными узлами. В режиме переключения резерва обмен реализуется только через один из коммутаторов, а остальные коммутаторы не используются до реконфигурации, производимой для замены отказавшего коммутатора на исправный (находящийся в резерве).

3. Оценка вероятности работоспособности системы, при использовании коммутаторов в режиме разделения нагрузки.

Оценим надежность (вероятность правильного функционирования) системы при условии работоспособности системы, заключающемся в обеспечении связи не менее чем между a₁ исправными узлами первой группы, включающей m₁ узлов и хотя бы a₂ исправными узлами из m₂  узлов второй группы при работоспособности связей хотя бы через a₃ из m₃ коммутаторов.

В предположении экспоненциального распределения времени между отказами вероятность работоспособности компонент сети определяется как

, ,,, при этом  - суммарные интенсивности отказов, соответственно, узла первой и второй групп, коммутатора и СА.

Точная оценка надежности исследуемых систем затруднена из-за сложной комбинаторного влияния распределения отказавших СА на работоспособность структуры. Рассмотрим некоторые приближенные верхние (оптимистические) и нижние оценки надежности системы, и определим их погрешности.

Вначале рассмотрим простейший случай – не учета влияния отказов СА на надежность системы. Вероятность работоспособности системы в этом случае определяется как

.

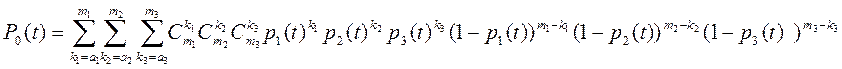Полученная оценка является оптимистической (верхней оценкой). Пренебрежение ненадежностью СА в ряде случаев может быть обусловлено необходимостью получения простой (грубой) верхней оценки или тем, что надежность СА по сравнению с другими сетевыми компонентами (например, серверами) значительно выше и часто практически мало влияет на ненадежность всей сети.

В частности, если система сохраняет работоспособность при исправности хотя бы одного узла каждого вида (a₁=1, a₂=1 и a₃=1) , то

 .            (1)

При нижней оценке надежности будем считать, что в работоспособной системе должно быть, по крайней мере, a₃ исправных коммутаторов, обеспечивающих связь с a₁ исправными  из m₁ узлами первой группы и a₂ исправными из m₂  узлами второй группы, причем для каждой из указанных связей СА, расположенные в соответствующих узлах, должны быть исправны. Пессимизм оценки обусловлен тем, что система  может быть работоспособна, помимо учитываемых в приближении состояний, и в состояниях, при которых связь между a₁ исправными узлами первой группы и a₂ исправными узлами второй группы обеспечивается всей совокупностью коммутаторов, а ни каждым из них в отдельности. Например, один коммутатор поддерживает связь между одной парой узлов, а остальные a₃-1 коммутаторов между всеми остальными парами.

С учетом сформулированных допущений нижнюю оценку вероятности работоспособности системы вычислим как:

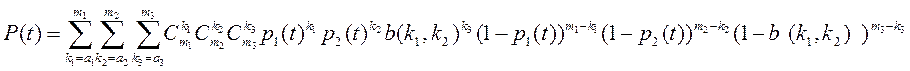, где b() вероятность исправного состояния коммутатора с учетом надежности сетевых адаптеров, поддерживающих его подключение не менее чем к a₁ узлам первой группы и к a₂ узлам второй группы, при условии исправности k₁ и k₂ узлов указанных групп; k₃ число исправных коммутаторов. Вероятность b() найдем по формуле:

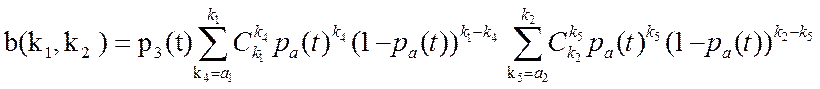,(2)

причем k₄ и k₅ число исправных СА, подключающих исправный коммутатор к исправным узлам первой и второй группы.

Погрешность предлагаемого приближения не хуже чем Δ₀(t)= P₀ (t)- P(t).

Если рассмотренная верхняя оценка является недостаточно точной (погрешность Δ₀(t) –хуже требуемой), то возможно ее уточнение.

При уточненной верхней оценке будем считать, что каждый исправный узел первой и второй группы через исправные СА должен быть подключен хотя бы к одному из исправных коммутаторов. Оптимистичность оценки обусловлена тем, что как исправные могут быть идентифицированы не работоспособные на самом деле состояния, при которых исправные узлы первой группы подключены к одним, а второй группы - к другим исправным коммутаторам (при этом связь между узлами разных групп не реализуема).

При уточненной верхней оценке вероятность работоспособности системы