Расчет предварительно напряженной плиты перекрытия. Конструктивная ширина панели. Предварительное напряжение арматуры

Диаметр, количество и размещение пустот назначены из расчета максимального снижения веса панели. Для удобства расшивки швов и во избежание местных околов на нижней поверхности панели предусматриваем устройство продольных фасок размерами 15 мм× 15 мм. Контуры боковых продольных поверхностей панелей устраиваем с выступами для улучшения заполнения швов бетоном.

     Конструктивное решение и основные геометрические размеры.

1)  Вид бетона – тяжелый, средней плотности 2200-2500 кг/м³ (п 2.1[16])

2)  Класс бетона В 30 (п 2.3[16])

3)  Коэффициент условий работы бетона γ_в2 = 0,9

4)   R_в,ser=22МПа; R_вt,ser=1,8МПа (приложение  III [12])

5)  R_в=17,0 МПа , R_вt=1,2 МПа  (приложение III [12])

6)  Е_в=29·10³ МПа (приложение  IV [12])

7)  Напрягающая арматура класса А_т V ; γ_s- коэффициент надежности по арматуре; γ_s=1,15 при расчете по предельным состояниям первой группы; γ_s=1- второй группы.

8)  R_s=680 МПа (приложение V[12])

9)  R_sn=R_s,ser=785 МПа (приложение V[12]), Е_s= 190·10³ МПа    

Для сварных сеток и каркасов используется холод. натянутая арматура проволока периодического профиля класса Вр-I.

Предварительное напряжение арматуры выполняется электротермическим способом на упоры. Бетон подвергается тепловой обработке.

Предварительное напряжение δ_sp=0,75; δ_sp=0,75·785=590 МПа.

δ_sp+ P ≤ R_s,ser      δ_sp – P ≥ 0,3 R_s,ser , где Р – при электротермическом способе натяжения арматуры принимается равным  30+360/L

590+30+360/6<785 МПа                   680<785 МПа

590-(30+360/6)>0,3·785 МПа            500>235,5 МПа условия выполняются

Вычисляем коэффициент точности напряжения арматуры:

γ_sp=1±Δγ_sp, где Δγ_sp при электротермическом способе натяжения арматуры принимается равным

Δγ_sp=0,5·P/δ_sp·(1+1/√n_p) где  n_p- число напрягаемых стержней в сечении элемента

Δγ_sp=0,5·90/590·(1+1/√6)=0,1, тогда коэффициент точности натяжения γ_sp=1-0,1=0,9; а при проверки по образованию трещин в верхней зоне плиты при обжатии принимаем  γ_sp-0,1+0,1=1,1.

Предварительное напряжение с учетом точности натяжения:           δ_sp=0,9·590= 531 МПа. Передаточную точность бетона устанавливаем так, чтобы при обжатии выполнялось условие δ_вр≤R_вр·0,95.

                                     Определение нагрузок

Таблица 5.1- Нагрузки на 1 м² перекрытия

P^н=2,00 кПа=200кг/м² (таблица 3, стр 5[17])

Коэффициенты надежности по нагрузке см(таблица 1, стр 3[17]); объемный вес материалов (приложение 3[5]).

Вес мозаичного пола qⁿ₁:

- керамзитобетон δ=35 мм, γ₀=1200 кг/м³;

- цементно-песчаная стяжка δ=20 мм, γ₀=1800 кг/м³;

- мозаичная смесь δ=20 мм, γ₀=2800 кг/м³.

Рисунок 5.1 – Поперечное сечение плиты     

   Приведение сечения панели к двутавровому осуществляются путем вычисления суммы ширины квадратных пустот эквивалентных по площади круглым (h_p=0,9d). Поэтому при ширине плиты по верху B^’_f=1460 мм и высоте  h=220 мм основные размеры двутаврового сечения следующие:

- ширина верхней полки   В’_f =1460 мм

- высота верхней полки h_f=(h-0,9d)/2=(220-0,9·159)/2=38 мм

- полная высота сечения h=220 мм

- ширина ребра В=В_f-n·d= 1460-7·0,9·159=458 мм

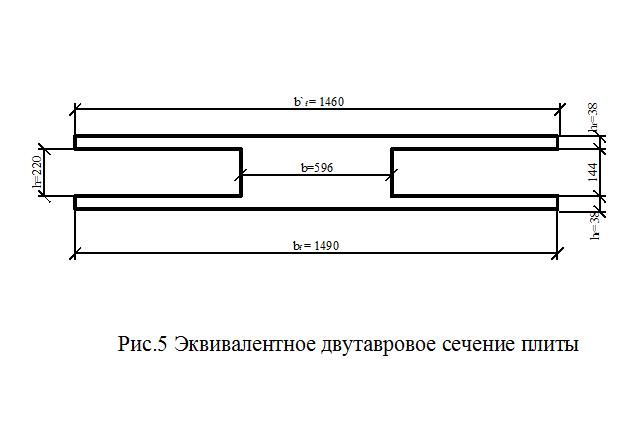Рисунок 5.3- Схема к определению расчетного пролета многопустотной плиты перекрытия.

Вычисляем расчетный пролет панели:

l₀=l_n-b-c_k-2 см=6000-300-100-20=5580, где l_n-пролет плиты; b и с_к- размеры ригеля.

К плите предъявляют требования третьей категории трещиностойкости.

Вычисляем  полную расчетную нагрузку на один погонный метр плиты перекрытия:        g=9,25·1,5=13,875 кН/м

Расчет прочности плиты по сечению нормальному к продольной оси:

М=ql²₀/8=13,875·5,58²/8=54,00 кН·м

Рабочая высота сечения h₀=h-a_s=220-30=190 мм

Предварительное напряжение с учетом полных потерь предварительно принимаем равным  δ_sp=0,7·531=372 МПа

Δδ_sp=1500·δ_sp/R_s-1200=1500·(372/680)-1200=-379<0   => Δδ_sp=0

Вычисляем напряжение в арматуре:

δ_s1=R_s+400-δ_sp=680+400-372=708 МПа

При коэффициенте γ_В2=0,9<1 напряжение δ_sc,u=500 МПа. Вычисляем коэффициент ω=a-0,008 Rв γ_В2=0,85-0,008·17·0,9=0,728

По формуле II.42 [12] вычисляем граничную относительную высоту сжатой зоны бетона ξ_R

         ξ_R=ω/1+δ_s1/δ_s2·(1-ω/1,1)=0,728/1+708/500(1-0,728/1,1)=0,49

Проверяем условие М≤ R_Вγ_В2В’_f h’_f (h₀-0,5h’_f)

54,00 кН·м ≤ 17·10³·0,9·1,46·0,038·(0,19-0,5·0,038)=145,15кН·м

54,00 кН·м< 145,15 кН·м => условие выполняется т.е. нейтральная ось находится в полке, а расчетное сечение имеет вид прямоугольника шириной В’_f=1460 мм.

А₀=М/R_В B’_f h₀² γ_В2=54,00/17·10³·0,9·1,46·0,19²=0,067

По таблице 3.1 [12] определяем ξ=0,07 , η=0,965

Для обеспечения перераспределения усилий должно соблюдаться условие  ξ<ξ_R и ξ<0,35

ξ=0,07<0,49       ξ=0,07<0,35     => условие соблюдается

γ_s6=η-(η-1)(2·ξ/ξ_R-1), где η=1,15 для арматуры класса А_т-V  

 γ_s6=1,15-(1,15-1)(2·0,07/0,49-1)=1,26 > η =1,15

Принимаем  γ_S6=1,15

Вычисляем требуемую площадь сечения продольной предварительно напряженной арматуры:

A_sp=M/η·γ_S6·R_S·h₀= 54,00/0,965·1,15·680·10³·0,19=3,766·10⁴ м²=3,77 см²

Принимаем 6Ø10 А_т-V с А_s=4,71 см² > 3,76 см²

Вычисляем коэффициент армирования μ

μ=А_sp/Вh₀=471/458·190=0,005>μ_min=0,0005

Расчет по прочности наклонных сечений

Вычисляем значение максимальной поперечной силы Q в плите перекрытия.

Q=q·l₀/2=13,875·5,58/2=38,71 кН

По формуле III.73[12] проверяем условие

Q≤0,3φω₁·φВ₁·R_В·В·h₀, где φω₁- коэффициент учитывающий влияние