Исследование влияния LC-параметров канала связи на форму сигнала. Анализ изменения синусоидального сигнала

2. Исследование влияния LC-параметров канала связи на форму сигнала.

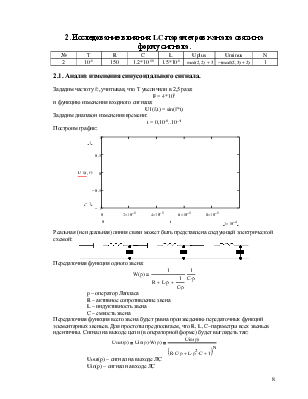
2.1. Анализ изменения синусоидального сигнала.

Зададим частоту f:, учитывая, что T увеличили в 2,5 раза:

F = 4*10⁵

и функцию изменения входного сигнала:

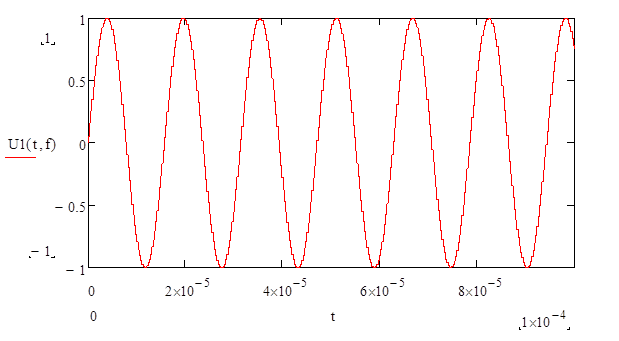
U1(f,t) = sin(f*t)

Зададим диапазон изменения времени:

t = 0,10^-8..10^--4

Построим график:

Реальная (не идеальная) линия связи может быть представлена следующей электрической схемой:

Передаточная функция одного звена:

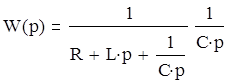
p – оператор Лапласа

R – активное сопротивление звена

L – индуктивность звена

С – емкость звена

Передаточная функция всего звена будет равна произведению передаточных функций элементарных звеньев. Для простоты предполагаем, что R, L, C–параметры всех звеньев идентичны. Сигнал на выходе цепи (в операторной форме) будет выглядеть так:

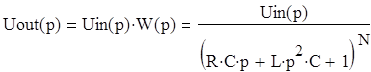
Uout(p) – сигнал на выходе ЛС

Uin(p) – сигнал на входе ЛС

N – количество элементарных звеньев цепи (N=1 в данном случае)

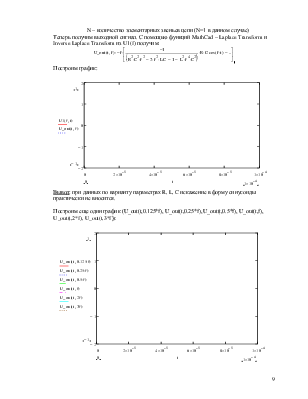
Теперь получим выходной сигнал. С помощью функций MathCad – Laplace Transform и Inverse Laplace Transform из U1(f) получим:

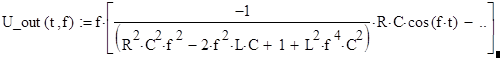
Построим график:

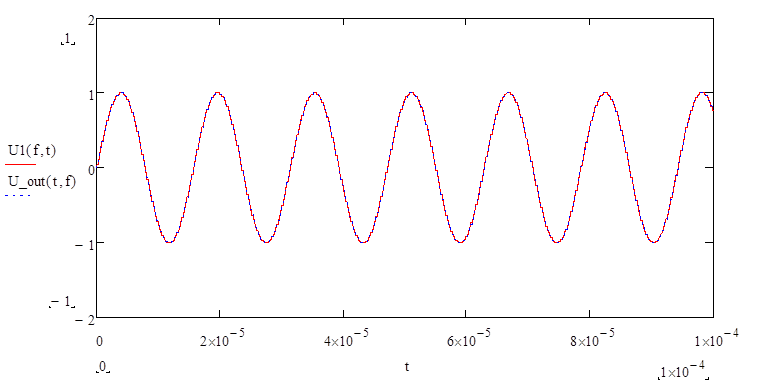
Вывод: при данных по варианту параметрах R, L, C искажение в форму синусоиды практически не вносится.

Построим еще один график (U_out(t,0.125*f), U_out(t,0.25*f), U_out(t,0.5*f), U_out(t,f), U_out(t,2*f), U_out(t,3*f)):

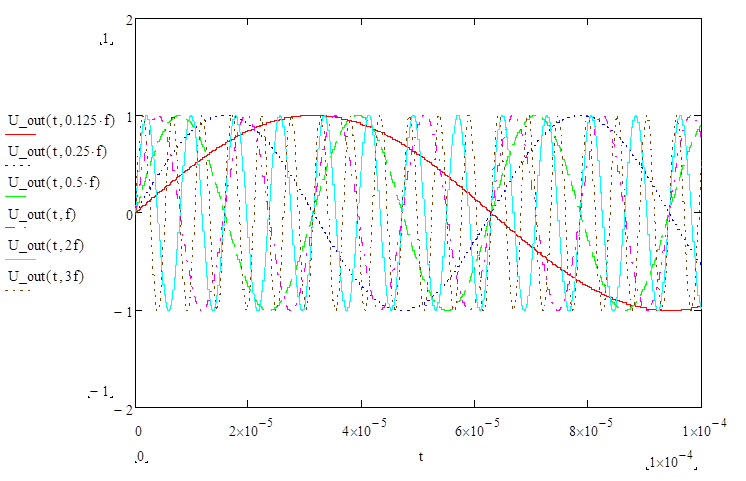
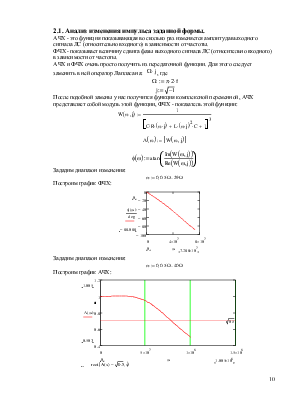
2.1. Анализ изменения импульса заданной формы.

АЧХ - это функция показывающая во сколько раз изменяется амплитуда выходного сигнала ЛС (относительно входного) в зависимости от частоты.

ФЧХ - показывает величину сдвига фазы выходного сигнала ЛС (относительно входного) в зависимости от частоты.

АЧХ и ФЧХ очень просто получить из передаточной функции. Для этого следует заменить в ней оператор Лапласа на:   , где

После подобной замены у нас получится функция комплексной переменной, АЧХ

представляет собой модуль этой функции, ФЧХ - показатель этой функции:

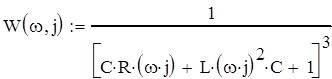
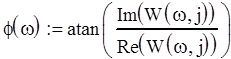
Зададим диапазон изменения:

Построим график ФЧХ:

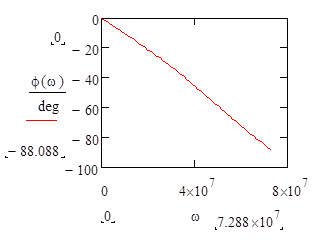
Зададим диапазон изменения:

Построим график АЧХ:

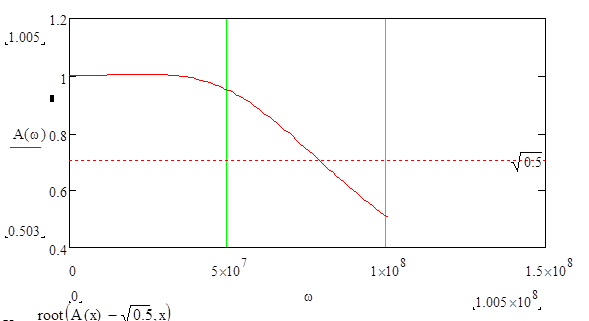
С помощью оператора root(f(x),x) найдем верхнюю границу полосы пропускания нашей ЛС. (Оператор root ищет ближайшую расположенную справа относительно первого приближения точку пересечения функции f(x) с осью х.):

Зная указанную граничную частоту, определим число гармоник К, которые имеет смысл рассчитывать:

Полученный результат округлим до ближайшего большего целого:

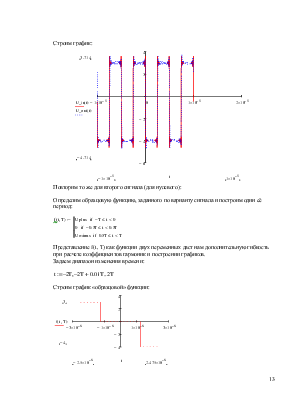
Определим образцовую функцию, заданного по варианту сигнала и построим один её период:

Представление f(t, T) как функции двух переменных даст нам дополнительную гибкость при расчете коэффициентов гармоник и построении графиков.

Задаем диапазон изменения времени:

Строим график «образцовой» функции:

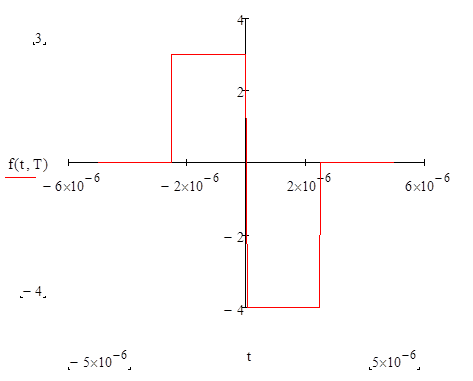
Зададим число отображаемых гармоник сигнала U_in:

  ,

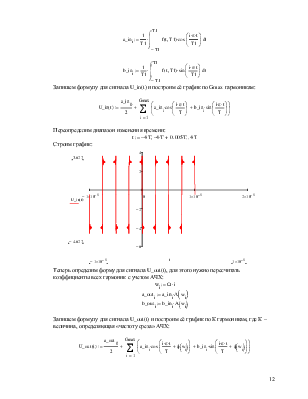
Запишем формулы для расчета коэффициентов этих гармоник.

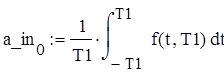
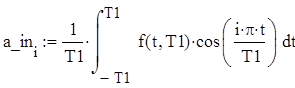
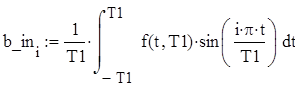
Запишем формулу для сигнала U_in(t) и построим её график по Gmax гармоникам:

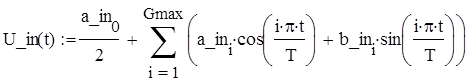
Переопределим диапазон изменения времени:

Строим график:

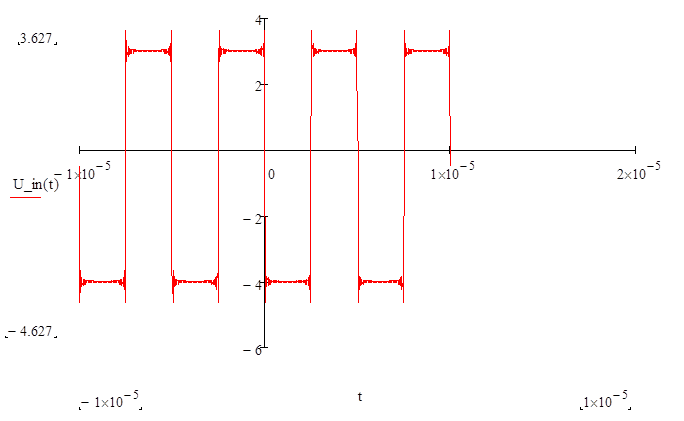
Теперь определим форму для сигнала U_out(t), для этого нужно пересчитать коэффициенты всех гармоник с учетом АЧХ:

Запишем формулу для сигнала U_out(t) и построим её график по К гармоникам, где К – величина, определяющая «частоту среза» АЧХ:

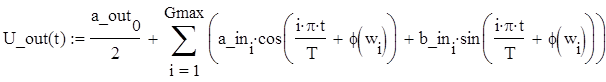
Строим график:

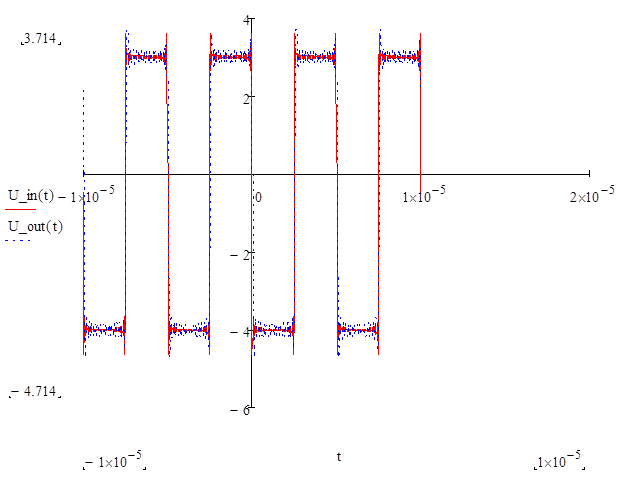
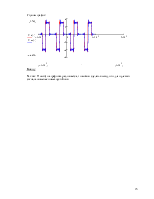
Повторим то же для второго сигнала (для нулевого):

Определим образцовую функцию, заданного по варианту сигнала и построим один её период:

Представление f(t, T) как функции двух переменных даст нам дополнительную гибкость при расчете коэффициентов гармоник и построении графиков.

Задаем диапазон изменения времени:

Строим график «образцовой» функции:

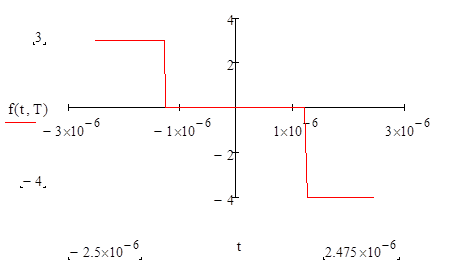
Зададим число отображаемых гармоник сигнала U_in:

  ,

Запишем формулы для расчета коэффициентов этих гармоник.

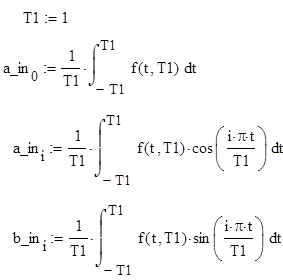
Запишем формулу для сигнала U_in(t) и построим её график по Gmax гармоникам:

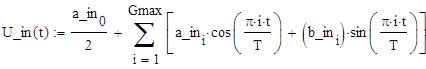
Переопределим диапазон изменения времени:

Строим график:

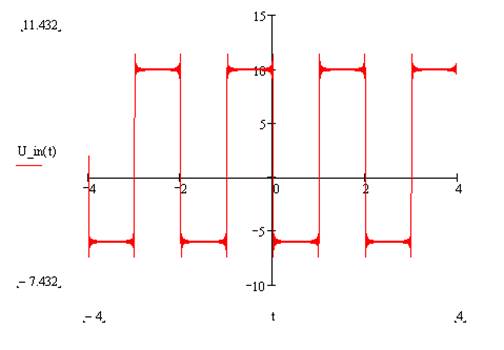
Теперь определим форму для сигнала U_out(t), для этого нужно пересчитать коэффициенты всех гармоник с учетом АЧХ:

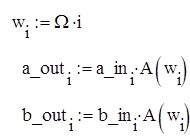
Запишем формулу для сигнала U_out(t) и построим её график по К гармоникам, где К – величина, определяющая «частоту среза» АЧХ:

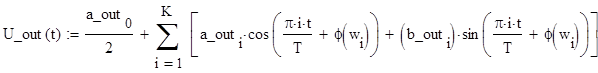
Строим график:

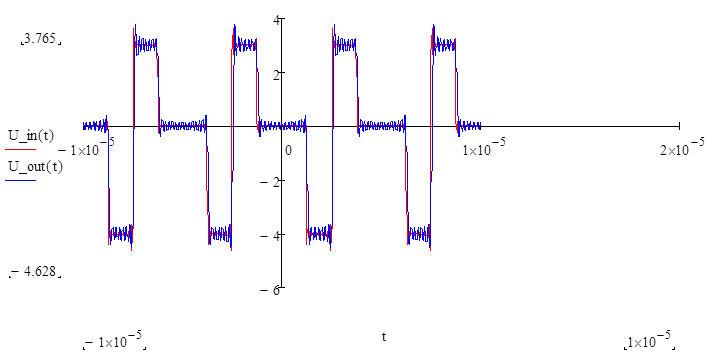
Вывод:

Так как U_out(t) на графиках различается, то можно сделать вывод, что для нулевого сигнала он менее помехоустойчив.