Исследование электрических цепей однофазного переменного тока. Электрическая цепь переменного синусоидального тока с последовательным соединением элементов

                    ЛАБОРАТОРНО-ПРАКТИЧЕСКАЯ РАБОТА №2

            «Исследование электрических цепей однофазного переменного тока»

1.             Цель работы:

1. Ознакомление с методикой построения схем и моделирования работы                          устройств в компьютерной лаборатории электротехники и электроники.

2. Исследование различных схем соединения электрических цепей

 переменного тока.

2.             Краткие теоретические сведения.

2.1.  Электрическая цепь переменного синусоидального тока с последовательным соединением элементов R, L, C (Рис.1).

                                                                       

°  R

 

                                  L      

 

                                                             C                  

                              °        

                                                                            

Рис.1

На практике электрическую цепь можно представить как последовательное             соединение трёх идеальных элементов: сопротивление, индуктивность иемкость.

Согласно II закону Кирхгофа для этой цепи имеем следующее уравнение в             комплексной форме

или                             .

Откуда - полное комплексное сопротивление [Ом].

Анализируя полученную формулу, можно констатировать, что ток I и все             напряжения U_R, U_L, U_C зависят от разности . То есть существуют три      соотношения элементов для данной цепи:

                                .

Рассмотрим их по порядку.

A.

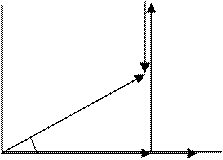
Построим на комплексной плоскости диаграмму напряжений (Рис.2).

                                                           +j

j                    +1

Рис.2

По теореме Пифагора модули напряжений и тангенс угла определены в виде    формул:

,                     .

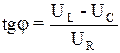Так как угол j > 0, то можно рассматривать характер цепи как активно-            индуктивный и заключить, что ток отстает от напряжения на угол j.

Коэффициент мощности получается 0 < cosj <1.

B.

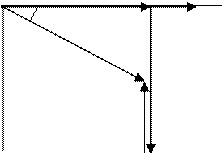
Диаграмма напряжений представлена на Рис.3.

                   +1

                                                                    j

-j

Рис.3.

Согласно теореме Пифагора формулы для модулей напряжений и тангенс угла    остаются такими же как и в предыдущем случае.

Однако угол j < 0 , и тогда можно рассматривать характер цепи как активно-       емкостной, а ток опережает напряжение на угол j.

Коэффициент мощности получается 0 < cosj <1.

C.

На комплексной плоскости имеем диаграмму напряжений (Рис.4):

                                                                  =                 +1

j = 0

   

-j

Рис.4.

Угол j = 0 и поэтому cosj = 1 , а ток в цепи будет максимальный

.

Основное равенство  называется условие резонанса, и этот случай            называется резонанс напряжений .

Зная, что  и , можно вывести формулу для резонансной             частоты

, откуда                                   

и так как пульсация , формула для резонансной частоты будет

.

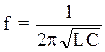Анализируя такую электрическую цепь, заключаем, что её характер можно менять,           варьируя частоту, индуктивность или емкость, переходя от индуктивного          характера к активному (резонанс) и далее к емкостному. График изменения тока       в цепи i = f(L или C или f),  в зависимости от этих параметров, представлен на           рисунке 5.

                                                           i

С (L или f)

C_рез

Рис.5.

2.2.          Электрическая цепь переменного синусоидального тока с                                         параллельным соединением элементов R, L, C (Рис.6).

°             I  –             –

                                                  U           R         I_R     L      I_L  C          I_C

 

                              °                   –             –

Рис.6

Можно представить также реальную электрическую цепь в виде трех идеальных     элементов сопротивления, индуктивности и емкости соединённых параллельно. В         этом случае I закон Кирхгофа дает следующую формулу в комплексной форме                                                           

и окончательно                    , где - комплексная, полная проводимость [1/Ом].

Из анализа полученной формулы видно, что все величины зависят от разности         и что существует три соотношения:

                                  .

Изучим эти три случая один за другим.

            A.

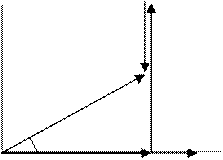
Диаграмма токов на комплексной плоскости иллюстрирует основные формулы        (Рис.7).

По теореме Пифагора модули токов и тангенс угла определены в виде этих             формул:

              .

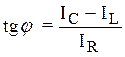                                                           +j

I_L

I_C

I

j      I_R             U      +1

Рис.7

Так как ток опережает напряжение на угол j, можно заключить, что             электрическая цепь имеет активно-емкостной характер, и коэффициент мощности      будет 0 < cosj <1.

B.

Диаграмма токов представлена на рисунке 8.

I_R                U      +1

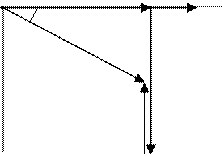                                                                    j

I

I_L

I_C

-j

Рис.8

Согласно теореме Пифагора формулы для модулей токов и тангенса угла             остаются такими же, как и в предыдущем случае.

Так как ток отстает от напряжения на угол j, можно заключить, что             электрическая цепь имеет активно-индуктивный характер, и коэффициент             мощности будет 0 < cosj <1.

C.

На комплексной плоскости представлена диаграмма токов (Рис.9):

Угол j = 0 и поэтому cosj = 1, а ток достигает своего минимального