Нам необходимо реализовать операцию умножения. Воспользуемся первым алгоритмом умножения, выбранным с учетом критерия (См п.1), так как он лучше по быстродействию, чем другие, в связи с тем, что сдвиг и передача информации совмещены во времени.
Алгоритм умножения с одновременным анализом младших разрядов множителя и сдвигом влево множимого.
Знак результата определяется сложением по модулю два знаков множителей
1. Происходит подготовка регистров.
2. Находится значение порядка результата.
3. Анализируется младший разряд множителя. Если он равен 1, то происходит сложение частичных сумм и множимого, если он равен 0, то переходим к пункту 4.
4. Происходит сдвиг множимого влево на 1 разряд.
5. Затем переходим к пункту 2. И так до тех пор пока не закончим умножение (число повторов определяется числом разрядов мантиссы множителя)
Для более точного описания алгоритма необходимо составить программу на ф-языке и представить ее в виде содержательной граф-схемы алгоритма.
Предварительно же необходимо рассчитать разрядную сетку. Расчет будем производить исходя из погрешности и диапазона представления чисел. (см. п.1 пояснительной записки.)
Расчет разрядной сетки:
Из диапазона представления чисел найдем число бит необходимых под порядок, а из погрешности число бит необходимых для мантиссы. Поскольку Критерием для нашего автомата является максимальное быстродействие, доведём число бит до кратного 8.
![]()
![]()
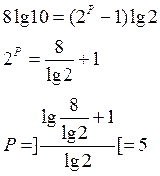
![]()
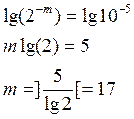
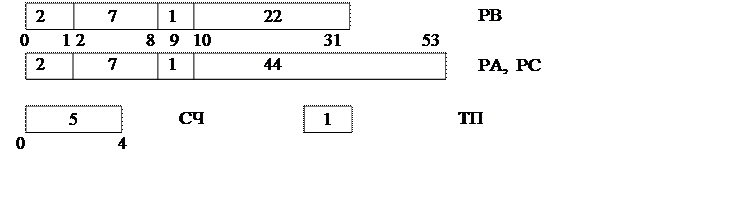 |
РА – множимое
РВ – множитель
РС – произведение
СЧ – счетчик
ТП – триггер переполнения
Теперь, когда разрядная сетка рассчитана, легко составить ГСА для нашего алгоритма (См лист 1 чертежа).
В нашем алгоритме можно выделить три основных части .
1) Нахождение порядка результата:
Если РА(0)=1, то переводим в дополнительный код порядок РА. Иначе ничего не меняем
Если РВ(0)=1, то находим порядок РС как сумму порядка РА с дополнительным кодом порядка РВ, Иначе Просто складываем порядки РА и РВ.
Если РС(0:1)=10 то результат слишком мал и попадает в область наших машинных нулей: РС=0, конец алгоритма.
2) Непосредственно алгоритм умножения:
Анализируем младший разряд регистра РВ. Если РВ(31)=1, то складываем мантиссы РС и РА, Иначе Сдвигаем РА влево на 1 разряд, а затем циклически сдвигаем РВ вправо на 1.
Уменьшаем значение счетчика на единицу
Сверяем значение счетчика с нулем. (Изначально счетчику присвоено значение 10, что соответствует числу разрядов РВ, то есть в тот момент, когда счетчик будет равен 0, регистр РВ вновь будет иметь значение множителя, и все его разряды будут проанализированы, следовательно, операция умножения закончится)
3) Нахождение знака результата, нормализация, проверка на переполнение.
Находим знак РС, как сумму по модулю два РА и РВ.
Проверяем мантиссу РС на нарушение нормализации «слева».
Проверяем код порядка РС. Если порядок отрицателен, то он сформирован в дополнительном коде и мы переводим его в прямой.
Проверяем знак порядка РС на комбинацию 01 (признак переполнения) и если переполнение присутствует, устанавливаем триггер переполнения в 1.
Теперь закодируем нашу ГСА (См. лист 1 чертежа):
Обозначим все операции через yi;
Обозначим все условия через xi;
Теперь составим таблицу микроопераций и управляющих сигналов им соответствующих.
|
Микрооперации |
||
|
y1 |
РС(0:53):= 0 |
|
|
y2 |
СЧ:= 10101 (21) |
|
|
y3 |
РА(0:8):=11.ù РА(2:8)+1 |
|
|
y4 |
РС(0:8):=РА(0:8)+РВ(0:8) |
|
|
y5 |
РС(0:8):=РА(0:8)+11.ù РВ(2:8)+1 |
|
|
y6 |
РС(9:53):=РС(9:53)+ РА(9:53) |
|
|
y7 |
РА(10:53):=L1(РА(10:53).РА(10)) |
|
|
y8 |
РB(10:31):=R1(PB(31).РВ(10:31)) |
|
|
y9 |
СЧ:= СЧ + 11111 |
|
|
y10 |
РС(9):= РА(9)ÅРС(9) |
|
|
y11 |
РС(9:53):=L1(PС(9:53).0) |
|
|
y12 |
РС(0:8):= PС(0:8)+111111111 |
|
|
y13 |
РС(0:8):=11.ù РС(2:8)+1 |
|
|
y14 |
ТП:=1 |
|
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.