Система с отказами. Граф переходов. Основные характеристики системы. Сегмент задания времени моделирования и вычислений

ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ

ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ

«МОСКОВСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ

 ПРИБОРОСТРОЕНИЯ И ИНФОРМАТИКИ»

филиал в г. Сергиев Посад

Кафедра ИТ-4

Отчет по лабораторной работе №3

по дисциплине «Моделирование»

Руководитель: преподаватель

Студентка:

спец. 230101

курс-4

группа ИТ4-06-01Д

Оценка

 

Подпись руководителя                ФИО руководителя

Сергиев Посад

2009 г.

Отчет по лабораторная работа №3

Вариант №3.

Выполнение работы.

Система с отказами

Рассматривается система М/М/1/0 – обработка сервером поступающих на него запросов при отсутствии буферной памяти. Поток заявок распределен по закону Пуассона с интенсивностью λ заявок в миллисекунду, время обработки заявки сервером распределено экспоненциально с интенсивностью µ заявок в мс.

Нарисуем граф переходов:

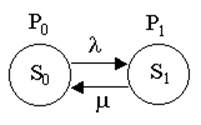Составим систему уравнений:

– λ P₀ + µ P₁ = 0,                                                                                      

λ P₀ – µ P₁ = 0,

P₀ + P₁ = 1.        

Решим систему уравнений с помощью системы GPSSWorld:

* Задание параметров

L_        EQU       4.12; интенсивность поступления заявок

MU_       EQU       4.69;   интенсивность обработки заявок

*

* Задание начальных значений вероятностей

P0_       EQU       1

P1_       EQU       0

*

* Интегрирование

P0_       Integrate(-L_#P0_+MU_#P1_);в скобках производная P0

P1_       Integrate(L_#P0_-MU_#P1_);в скобках производная P1

* Задание времени интегрирования

GENERATE  10

TERMINATE 1

START   1

Thursday, November 06, 2008 09:09:10 

START TIME           END TIME  BLOCKS  FACILITIES  STORAGES

0.000             10.000     2        0          0

NAME                       VALUE 

L_                              3.560

MU_                             4.010

P0_                             0.530

P1_                             0.470

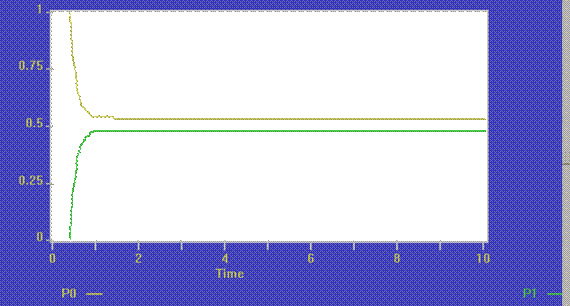
1. Определить аналитически следующие характеристики системы:

§  – коэффициент загрузки сервера: ρ = λ/µ=0,888;

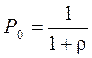§   =0,53– вероятность простоя системы.

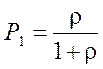§  =0,47 – вероятность отказа в обслуживании (прибор занят);

§  q = 1 – P₁ =0,53 – относительная пропускная способность – доля обслуженных заявок;

§  А = λq =1,887– абсолютная пропускная способность – среднее число обслуженных заявок в единицу времени.

*         Сегмент задания параметров системы

L_        EQU       3.56; интенсивность заявок

MU_       EQU       4.01; интенсивность обслуживания

*

*         Основной сегмент

GENERATE (Exponential(1,0,(1/L_))); Генерация заявок

*                                                 с интенсивностью L_ заявок в секунду

*

GATE NU  SERV,POTERI; Проверка, если сервер занят, то

*                                    отправляем заявку в потери (к блоку с меткой POTERI)

*

SEIZE  SERV; Иначе занимаем сервер

ADVANCE (Exponential(1,0,(1/MU_))); на время обработки

RELEASE  SERV; после обработки заявки освобождаем сервер

TERMINATE;  и удаляем обработанную заявку

POTERI  SAVEVALUE  POTER+,1; Добавляем 1 к потерям и

TERMINATE;  удаляем потерянную заявку 

*

*         Сегмент задания времени моделирования и вычислений

GENERATE 3600 000 ; Задаем время моделирования - один час

SAVEVALUE RO_(L_/MU_)

SAVEVALUE P_OTK (X$POTER/N1); Определяем вероятность потерь

SAVEVALUE P_0 (1-X$P_OTK); и вероятность обработки заявок

SAVEVALUE Q_ (X$P_0)

SAVEVALUE A_ (L_#X$Q_)

TERMINATE 1; Стандартное окончание

START  1;           времени моделирования

GPSS World Simulation Report - Untitled Model 1.15.1

Thursday, November 06, 2008 09:42:32 

START TIME           END TIME  BLOCKS  FACILITIES  STORAGES

0.000           3600.000    15        1          0

NAME                       VALUE 

A_                          10008.000

L_                              3.560

MU_                             4.010

POTER                       10003.000

POTERI                          7.000

P_0                         10006.000

P_OTK                       10005.000

Q_                          10007.000

RO_                         10004.000

SERV                        10002.000

LABEL              LOC  BLOCK TYPE     ENTRY COUNT CURRENT COUNT RETRY

1    GENERATE         12590             0       0

2    GATE             12590             0       0

3    SEIZE             6764             0       0

4    ADVANCE           6764             1       0

5    RELEASE           6763             0       0

6    TERMINATE         6763             0       0

POTERI              7    SAVEVALUE         5826             0       0

8    TERMINATE         5826             0       0

9    GENERATE             1             0       0

10    SAVEVALUE            1             0       0

11    SAVEVALUE            1             0       0

12    SAVEVALUE            1             0       0

13    SAVEVALUE            1             0       0

14    SAVEVALUE            1             0       0

15    TERMINATE            1             0       0

FACILITY         ENTRIES  UTIL.   AVE. TIME AVAIL. OWNER PEND INTER RETRY DELAY

SERV              6764    0.469       0.250  1    12591    0    0     0      0

SAVEVALUE               RETRY       VALUE

POTER                    0       5826.000                           

RO_                      0          0.888                           

P_OTK                    0          0.463                           

P_0                      0          0.537                           

Q_                       0          0.537                           

A_                       0          1.913                           

FEC XN   PRI         BDT      ASSEM  CURRENT  NEXT  PARAMETER    VALUE

12592    0        3600.004   12592      0      1

12591    0        3600.005   12591      4      5

12593    0        7200.000   12593      0      9

Результаты, полученные в результате моделирования, совпадают с результатами, полученными аналитическим методом, следовательно система смоделирована правильно.

Система с ограниченной очередью

Рассматривается система М/М/1/m, где m – допустимая длина очереди – обработка сервером поступающих на него запросов при ограниченном объеме буферной памяти. Поток заявок распределен по закону Пуассона с интенсивностью λ заявок в миллисекунду, время обработки заявки сервером распределено экспоненциально с интенсивностью µ заявок в мс, допустимая длина очереди m.  (m=3).

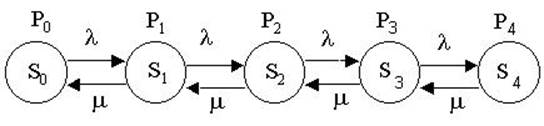Нарисуем граф переходов:

Составим систему уравнений:

–λ P₀ + µ P₁ = 0;                               

λ P₀ –( λ+µ) P₁ +µ P₂ = 0;                 

λ P₁ – ( λ +µ) P₂ + µ P₃ = 0;              

λ P₂ – ( λ +µ) P₃ + µ P₄ = 0;              

λ P₃ – µ P₄ = 0;                                  

P₀ + P₁ + P₂ + P₃ + P₄ = 1.                

Решим систему уравнений с помощью системы GPSSWorld:

* Задание параметров

L_        EQU       3.56; интенсивность поступления заявок

MU_       EQU       4.01;   интенсивность обработки заявок

*

* Задание начальных значений вероятностей

P0_       EQU       1

P1_       EQU       0

P2_       EQU       0

P3_       EQU       0

P4_       EQU       0

* Интегрирование

P0_       Integrate(-L_#P0_+MU_#P1_);в скобках производная P0

P1_       Integrate(L_#P0_-(L_+MU_)#P1_+MU_#P2_);в скобках производная P1

P2_       Integrate (L_#P1_-(L_+MU_)#P2_+MU_#P3_);в скобках производная P2

P3_       Integrate (L_#P2_-(L_+MU_)#P3_+MU_#P4_);в скобках производная P3

P4_       INTEGRATE (L_#P3_-MU_#P4_); в скобках производная P4

* Задание времени интегрирования

GENERATE  10

TERMINATE 1

START   1

Thursday, November 06, 2008 10:05:21 

START TIME           END TIME  BLOCKS  FACILITIES  STORAGES

0.000             10.000     2        0          0

NAME                       VALUE 

L_                              3.560

MU_                             4.010

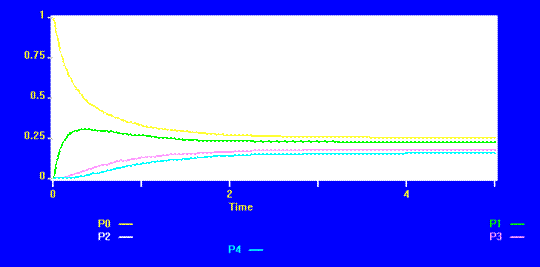
P0_                             0.250

P1_                             0.222

P2_                             0.197

P3_                             0.175

P4_                             0.155

1. Определить аналитически следующие характеристики системы:

Определить аналитически следующие характеристики системы:

§  – коэффициент загрузки сервера: ρ = λ/µ=0,888;

§  – вероятности состояний сервера (состояние определяется числом заявок в системе):

§  Вероятность простоя системы:

P₀= (1 – ρ)/(1 – ρ^m+2)=0,25.

§  Вероятности других состояний системы:

P₁ = ρ P₀₌0,222;

P₂ = ρ² P₀=0,197;  

P₃ = ρ³ P₀ =0,175 ;  

P₄ = ρ⁴ P₀ =0,155;

P₀ + P₁ + P₂ + P₃ + P₄ = 1.                

§  Вероятность потерь:

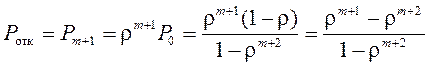=0,155,  ρ<>1.

§  Относительная пропускная способность  (доля обслуженных заявок):

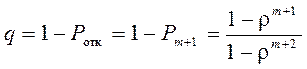=0,845.

§  Абсолютная пропускная способность:

А = λq=3,01  – интенсивность потока обслуженных заявок.

§  Среднее число заявок в очереди  :

= ρ P₀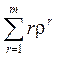=1,013.

§  Среднее число заявок на обслуживании:

 = (ρ – ρ^m+2)/(1 – ρ^m+2)=0,75.

§  Среднее число заявок в системе (в очереди и на обслуживании):

=1,763.

§  Среднее время ожидания в очереди:

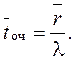=0,285

§  _обс=1/µ=0,249

§  Среднее время пребывания заявки в системе:

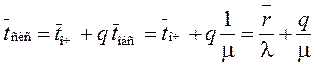=0,495

Смоделировать в течение 1 часа работу простейшей одноканальной СМО с ограничением на длину очереди(m=3):

L_ EQU 3.56

Mu_ EQU 4.01

M_ EQU 3

CAS EQU 1

GENERATE (Exponential(1,0,(1/L_)))

TEST E  Q1,3,met1

SAVEVALUE  POTER+,1

TERMINATE

met1 test E  Q1,1,met2

SAVEVALUE  Q_1+,1  

met2 test E  ((~F1)&(Q1=0)),1,met3

SAVEVALUE  Q0f0_+,1

met3 test E  ((F1)&(Q1=0)),1,met4

SAVEVALUE  Q0f1_+,1

met4 test E Q1,2,met6

SAVEVALUE  Q_2+,1

met6 test E  Q1,0,met5

SAVEVALUE  Q0_+,1

met5 QUEUE  1

SEIZE  1

DEPART  1

ADVANCE  (Exponential(2,0,(1/Mu_)))

RELEASE  1

TERMINATE 

GENERATE 3600 0000;

SAVEVALUE RO_,(L_/Mu_)

SAVEVALUE  Q_,(1-x$POTER/N1)

SAVEVALUE  AABS,(L_#X$Q_)

SAVEVALUE  P_0,(X$q0f0_/n1)

SAVEVALUE  P_1,(X$q0f1_/n1)

SAVEVALUE  P_2,(X$Q_1/n1)

SAVEVALUE  P_3,(X$Q_2/n1)

SAVEVALUE  P_otk,(x$POTER/N1)

SAVEVALUE  P_sum,(x$P_0+x$P_1+x$P_2+X$P_3+x$P_otk)

TERMINATE 1; Стандартное окончание

START  1;          времени моделирования

GPSS World Simulation Report - Untitled Model 1.21.1

Thursday, November 06, 2008 11:02:31 

START TIME           END TIME  BLOCKS  FACILITIES  STORAGES

0.000           3600.000    31        1          0

SAVEVALUE               RETRY       VALUE

Q0F0_                    0       3216.000                           

Q0_                      0       6058.000                           

Q0F1_                    0       2842.000                           

Q_1                      0       2442.000                            

Q_2                      0       2205.000                           

POTER                    0       1912.000                           

RO_                      0          0.888                           

Q_                       0          0.848                           

AABS                     0          3.021                           

P_0                      0          0.255                           

P_1                      0          0.225                            

P_2                      0          0.194                           

P_3                      0          0.175                           

P_OTK                    0          0.152                           

P_SUM                    0          1.000                           

Результаты, полученные в результате моделирования, совпадают с результатами, полученными аналитическим методом, следовательно система смоделирована правильно.

Система без потерь

Исследование системы без потерь проводится в два этапа: сначала определяется максимальная длина очереди, а затем определяются вероятности состояний, как для системы с ограниченной очередью (но без ограничения очереди).

Первый этап:

Определим макс. длину очереди.

*       Сегмент задания параметров системы

K_      EQU     5; коэффициент, введенный для уменьшения r_мах

L_      EQU3.56; лямбда

MU_     EQU4.01#K_; мю новое

*

*       Основной сегмент

GENERATE (Exponential(1,0,(1/L_))); Генерация заявок

*                              с интенсивностью L_ заявок в секунду

QUEUESERV ; Встаем в очередь. Если сервер свободен,

SEIZESERV ; то занимаем его

DEPARTSERV ; и освобождаем место в очереди

ADVANCE (Exponential(1,0,(1/MU_))); обрабатываем заявку

RELEASESERV; после обработки заявки освобождаем сервер

TERMINATE;  и удаляем обработанную заявку

POTERISAVEVALUEPOTER+,1; Добавляем 1 к потерям и

TERMINATE;  удаляем потерянную заявку 

*

*       Сегмент задания времени моделирования и вычислений

GENERATE 3600; Задаем время моделирования - один час

TERMINATE 1; Стандартное окончание

START  1; времени моделирования

QUEUE              MAX CONT. ENTRY ENTRY(0) AVE.CONT. AVE.TIME   AVE.(-0) RETRY

SERV                4    0  12794  10446     0.039      0.011      0.060   0

При прогоне программы получаем  r_мах = 4, поэтому в системе будет 6 состояний S0, S1, S2, S3, S4, S5.

P5

Второй этап:

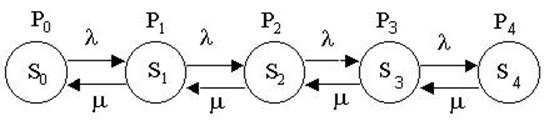
Составим систему уравнений:

–λ P₀ + µ P₁ = 0;                               

λ P₀ –( λ+µ) P₁ +µ P₂ = 0;                 

λ P₁ – ( λ +µ) P₂ + µ P₃ = 0;              

λ P₂ – ( λ +µ) P₃ + µ P₄ = 0;              

λ P₃ – ( λ +µ) P₄ + µ P₅ = 0;              

λ P₄ – µ P₅ = 0;                                  

P₀ + P₁ + P₂ + P₃ + P₄ + P₅= 1.                

Решим систему уравнений с помощью системы GPSSWorld:

* Задание параметров

K_        EQU       5; коэффициент, введенный для уменьшения r_мах

L_        EQU       3.56; лямбда

MU_       EQU       4.01#5;   мю новое

*

* Задание начальных значений вероятностей

P0_       EQU       1

P1_       EQU       0

P2_       EQU       0

P3_       EQU       0

P4_       EQU       0

P5_       EQU       0

* Интегрирование

P0_ INTEGRATE (-L_#P0_+MU_#P1_); в скобках производная P0

P1_       Integrate(L_#P0_-(L_+MU_)#P1_+MU_#P2_);в скобках производная P1

P2_       Integrate(L_#P1_-(L_+MU_)#P2_+MU_#P3_);в скобках производная P2

P3_       Integrate(L_#P2_-(L_+MU_)#P3_+MU_#P4_);в скобках производная P3

P4_       Integrate(L_#P3_-(L_+MU_)#P4_+MU_#P5_);в скобках производная P4

P5_       INTEGRATE (L_#P4_-MU_#P5_); в скобках производная P5

* Задание времени интегрирования

GENERATE  10

TERMINATE 1

START   1

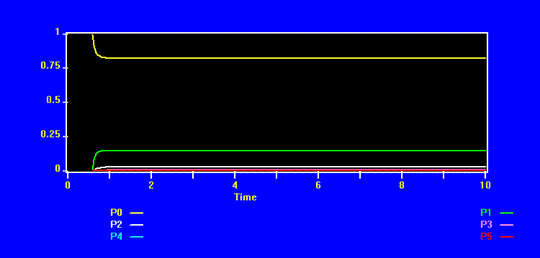
NAME                       VALUE 

K_                              5.000

L_                              3.560

MU_                            20.050

P0_                             0.822

P1_                             0.146

P2_                             0.026

P3_                             0.005

P4_                             0.001

P5_                             0.000

Рассматривается простейшая одноканальная СМО без ограничения длины очереди – обработка сервером поступающих на него запросов при неограниченном объеме буферной памяти (конечно, объем буферной памяти ограничен, но он больше возможной максимальной длины очереди). Поток заявок распределен по закону Пуассона с интенсивностью λ заявок в миллисекунду, а время обработки заявки сервером распределено экспоненциально с интенсивностью µ заявок в мс.

Другими словами рассматривается система М/М/1/, где  – неограниченная очередь.

1. Определить аналитически следующие характеристики системы:

§  – коэффициент загрузки сервера: ρ = λ/µ=3,56/4,01*5=0,178;

§  – вероятности состояний сервера (состояние определяется числом заявок в системе):

§   = 1 – ρ=0,822– вероятность простоя (заявок нет);

§  P₁ = ρ  = ρ(1 – ρ)=0,146 – одна заявка (обслуживается, очереди нет);

§  P₂ = ρ² = ρ²(1 – ρ)=0,0026 – две заявки (одна обслуживается, вторая