Система без потерь. Граф переходов системы. Программа имитационного моделирования. Система дифференциальных уравнений

ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ

ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ

«МОСКОВСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ

 ПРИБОРОСТРОЕНИЯ И ИНФОРМАТИКИ»

филиал в г. Сергиев Посад

Кафедра ИТ-4

Курсовая работа

по дисциплине «Моделирование»

Руководитель: преподаватель

Студентка:

спец. 230101

курс-4

группа ИТ4-05-01Д

Оценка

Подпись руководителя                ФИО руководителя

Сергиев Посад

2008 г.

Вариант №13.

Данная курсовая работа является также отчетом лабораторной работы № 4.

Задание.

1. Нарисовать структурную  схему.

2.  Определить число состояний.

3.  Составить систему уравнений (алгебраические и дифференциальные).

4.  Составить программу интегрирования.

5.   Составить программу имитационного моделирования.

Система без потерь

На вход четырехпроцессорной ВС с неограниченной очередью поступает пуассоновский поток заявок с интенсивностью 2 заявки в минуту. Время обработки заявки в одном процессоре равно 0.6 минут (экспоненциальное распределение). Система М/М/4/.

Найти вероятность обслуживания тех заявок, которые поступают в систему при условии отсутствия очереди и вероятности других состояний системы, среднюю длину очереди, среднее число занятых процессоров, среднее время ожидания в очереди и обслуживания в системе.

Система без потерь работает в стационарном режиме, поэтому очередь ограничена и путем проверки состояний процессоров обнаружили, что очередь равна 2. В дальнейшем проводим исследования для системы с очередью q = 2.

 Структурная схема.

 Граф переходов системы.

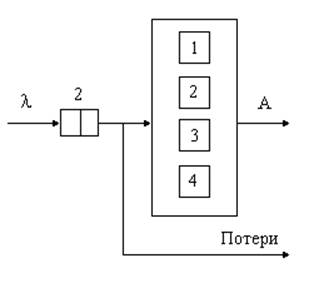
Состояния системы:

S₀- все процессоры свободны;

S₁- один процессор работает;

S₂- два процессора работают;

S₃- три процессора работают;

S₄- четыре процессора работают.

Система дифференциальных уравнений:

- λP₀(t) + μP₁(t);

λP₀(t) - ( λ+μ)P₁(t) + 2μP₂(t);

λP₁(t) - (2μ+λ)P₂(t) +3μP₃(t);

λP₂(t) - (3μ+λ)P₃(t) +4μP₄(t);

λP₃(t) - (4μ+λ)P₄(t) +4μP₅(t);

λP₄(t) - (4μ+λ)P₅(t) +4μP₆(t);

λP₅(t) - 4μP₆(t).

Система алгебраических уравнений:

S₀:      - λP₀ + μP₁=0;

S₁:         λP₀ - ( λ+μ)P₁ + 2μP₂=0;

S₂:         λP₁ - (2μ+λ)P₂ +3μP₃=0;

S₃:         λP₂ - (3μ+λ)P₃ +4μP₄=0;

S₄:         λP₃ - (4μ+λ)P₄ +4μP₅=0;

S₅:         λP₄ - (4μ+λ)P₅ +4μP₆=0;

S₆:         λP₅ - 4μP₆=0.

Аналитический расчет характеристик.

1) 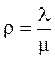= 2/1.8 = 1,111

2) Доля обслуженных заявок

q = 1 – система без потерь.

3) Абсолютная пропускная способность

А = .

4) Вероятность того, что все приборы свободны

P₀ = 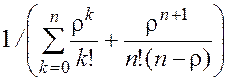 = 0,328.

5) Вероятности других состояний системы

(состояния определяются числом заявок в системе k)

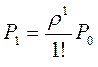= 0,364; при k – очереди нет,

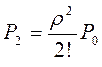= 0,202;

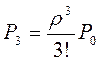= 0,075;

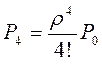= 0,021;

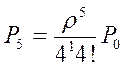= 0,006_, при ,  r – длина очереди.

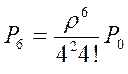= 0,002.

6) Средняя длина очереди.

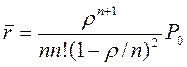= 0,011.

7) Среднее время ожидания в очереди

 =  = 0,006.

8) Вероятность того, что все приборы заняты

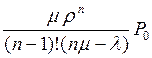 =  = 0,028.

9) Вероятность обслуживания заявки без помещения ее в очередь

P₀₀ = 1–P_зан = 0,972.

10) Среднее число занятых приборов

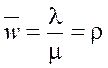= 1,111. 

11) Среднее число заявок в системе

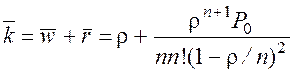 = 1,122.

12) Среднее время нахождения заявки в системе (время отклика)

    =  0,561.

Программа модели M/M/4/

* Программа модели M/M/4/ – 4 процессора и неограниченная очередь

* лямбда = 2, мю = 1.8

L_ EQU 2

MU_  EQU 1.8

SYST                              EQU                          1

SYST                              STORAGE   4; четыре  процессора

GENERATE   (Exponential(1,0,(1/L_)))

TEST E   ((S1=0)&(Q1=0)),1,MET_1

SAVEVALUE   10+,1

MET_1        TEST E   ((Q1=0)&~SF1),1,MET_2;

SAVEVALUE   1+,1

MET_2        TEST E   ((Q1=0)&(S1=1)),1,MET_3;

SAVEVALUE   2+,1

MET_3        TEST E   ((Q1=0)&(S1=2)),1,MET_4;

SAVEVALUE   3+,1

MET_4        TEST E   ((Q1=0)&(S1=3)),1,MET_5;

SAVEVALUE   4+,1

MET_5        TEST E   ((Q1=0)&(S1=4)),1,MET_6;

SAVEVALUE   5+,1

MET_6        TEST E   ((Q1=1)&(S1=4)),1,MET_7;

SAVEVALUE   6+,1

MET_7        TEST E   ((Q1=2)&(S1=4)),1,MET_8;

SAVEVALUE   7+,1

MET_8        QUEUE 2

QUEUE   1

ENTER   1

DEPART   1

ADVANCE  (Exponential(1,0,(1/MU_)))

LEAVE   1

DEPART   2

TERMINATE

generate  1000

savevalue  P_0,(x10/n1)

savevalue  P_00,(x1/n1)

savevalue  P_1,(x2/n1)

savevalue  P_2,(x3/n1)

savevalue  P_3,(x4/n1)

savevalue  P_4,(x5/n1)

savevalue  P_5,(x6/n1)

savevalue  P_6,(x7/n1)

savevalue  RE_,(0.034#x$P_0)

savevalue  W_,(L_/MU_)

savevalue  T_och,(X$RE_/L_)

savevalue K_,(X$W_+X$RE_)

savevalue  T_sys,(X$K_/L_)

savevalue  P_SUM,(X$P_0+X$P_1+X$P_2+X$P_3+X$P_4+X$P_5+X$P_6)

terminate   1

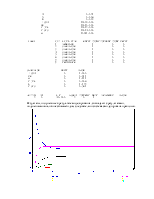
START   1

Стандартный отчет

GPSS World Simulation Report - Untitled Model 1.19.1

Tuesday, December 02, 2008 00:22:39 

START TIME           END TIME  BLOCKS  FACILITIES  STORAGES