Определение:Три вектора ![]() называют
компланарными, если они лежат в одной плоскости или параллельных плоскостях
одной плоскости.
называют
компланарными, если они лежат в одной плоскости или параллельных плоскостях
одной плоскости.
Теорема:Для того, чтобы три вектора ![]() были компланарными необходимо и
достаточно, чтобы их смешанное произведение было равно нулю.
были компланарными необходимо и
достаточно, чтобы их смешанное произведение было равно нулю.
![]()
Примеры решения задач.
Пример 1:
Даны вершины треугольника А(2;-3;1) В(1;2;0) С(4;-1;0). Найти его внутренний угол А.
Решение:
Для решения задачи сделаем схематический чертёж Рис 3.6
![]()
 В
В
![]() А
А
С
Рис. 3.6
Найдём проекции векторов ![]() и
и ![]() :
из координат конца вектора, вычитаем соответствующие координаты начала вектора.
:
из координат конца вектора, вычитаем соответствующие координаты начала вектора.
![]()
![]()
далее используем формулу для нахождения косинуса угла между векторами, заданными своими координатами
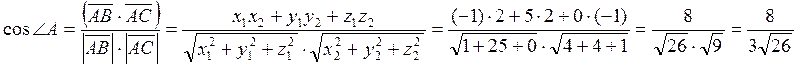
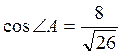
Далее по таблице находим угол А.
Пример 2:
Найти проекцию вектора ![]() на ось составляющую одинаковые
углы с осями координат.
на ось составляющую одинаковые
углы с осями координат.
![]()
Решение:
Воспользуемся формулой связывающей направляющие косинусы вектора.
![]()
Так как ось составляет
одинаковые углы с осями координат то, ![]() ,
тогда
,
тогда
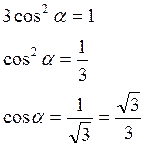
Так как направляющие
косинусы являются проекциями единичного вектора, направленного вдоль этой оси.
Обозначим этот вектор ![]() . Тогда проекции этого
вектора:
. Тогда проекции этого
вектора: 
Далее воспользуемся формулой для нахождения проекции одного вектора на другой
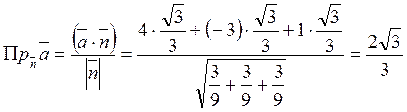
Пример 3:
При каком значении k векторы ![]() и
и ![]() перпендикулярны.
перпендикулярны.
Решение:
Так как векторы ![]() и
и ![]() перпендикулярны, то
перпендикулярны, то ![]() . Используем формулу для
нахождения скалярного произведения векторов, заданных своими проекциями.
. Используем формулу для
нахождения скалярного произведения векторов, заданных своими проекциями.
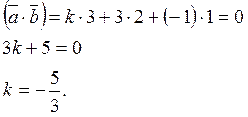
Пример 4:
Найти вектор ![]() , зная что он перпендикулярен
векторам
, зная что он перпендикулярен
векторам ![]()
![]() и
удовлетворяет условию
и
удовлетворяет условию ![]() , где вектор
, где вектор ![]() .
.
Решение:
Обозначим проекции
вектора ![]() неизвестными x,y,z
неизвестными x,y,z
![]() , используя условие
перпендикулярности векторов, имеем
, используя условие
перпендикулярности векторов, имеем
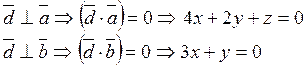
Таким образом, имеем
 значит искомый вектор
значит искомый вектор ![]() .
.
Пример 5:
Даны точки А(3;2;1);
В(-1;0;2); С(4;1;0); D(2;1;-1). Найти ![]()
Решение:
Найдём проекции векторов
![]() и
и ![]()
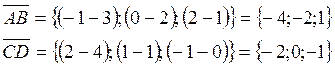
далее воспользуемся формулой вычисления проекции одного вектора на другой
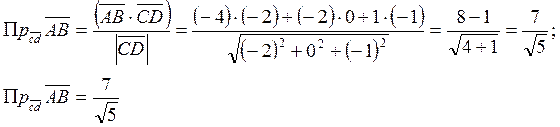
Пример 6:
Даны вершины треугольника A(2;0;-3); B(1;2;-5); C(3;-1;2). Найти высоту треугольника, опущенную из вершины В.
Решение:
Сделаем схематический чертёж Рис 3.7
 В
В
h
А
К С
Рис 3.7
Найдем проекции векторов ![]() и
и ![]()
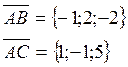
используя
геометрический смысл векторного произведения, найдём площадь ![]()

с другой стороны из школьного курса геометрии известно, что 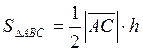 тогда имеем равенство:
тогда имеем равенство:
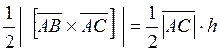
и тогда: 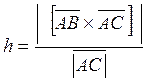 .
.
Найдем вектор векторного
произведения ![]() в случае если векторы заданы
своими проекциями.
в случае если векторы заданы
своими проекциями.
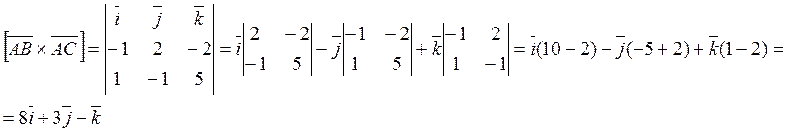 Таким образом вектор
Таким образом вектор ![]() имеет проекции:
имеет проекции: ![]() .
.
Зная проекции вектора легко находим его модуль.
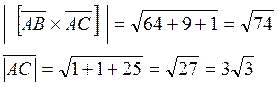
Таким образом, высота:
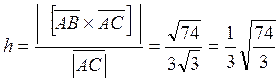 .
.
Пример 7:
Найти (х) при котором
векторы ![]() ;
; ![]()
![]() будут компланарны.
будут компланарны.
Решение:
Используя необходимое и
достаточное условие компланарности трёх векторов, можем записать, что смешанное
произведение векторов ![]() должно равняться нулю.
должно равняться нулю.
![]()
или для случая, когда векторы заданы своими проекциями:

Раскроем определитель по 1ой строке
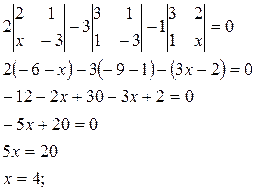
Пример 8:
Доказать, что четыре точки A(2;-3;1); B(3;-4;3); C(5;-1;2); D(6;-2;4) лежат в одной плоскости.
Решение:
Найдём проекции векторов
![]()
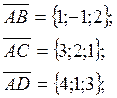
если мы докажем, что векторы ![]() лежат в одной плоскости, то это
будет означать, что точки A,B.C,D лежат в одной плоскости. Векторы
лежат в одной плоскости, то это
будет означать, что точки A,B.C,D лежат в одной плоскости. Векторы ![]() компланарны или лежат в одной
плоскости в случае, если их смешанное произведение равно нулю. Рассмотрим
смешанное произведение векторов
компланарны или лежат в одной
плоскости в случае, если их смешанное произведение равно нулю. Рассмотрим
смешанное произведение векторов ![]() заданных
своими проекциями.
заданных
своими проекциями.
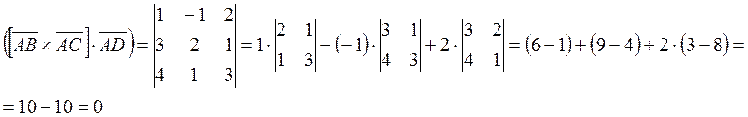
Таким образом, смешанное произведение трёх векторов ![]() равно нулю, а это значит они
лежат в одной плоскости, а следовательно и точки A,B.C,D лежат в одной плоскости,
что и требовалось доказать.
равно нулю, а это значит они
лежат в одной плоскости, а следовательно и точки A,B.C,D лежат в одной плоскости,
что и требовалось доказать.
Пример 9:
Найти высоту пирамиды опущенной из вершины D, если заданы координаты вершин пирамиды А(1;6;-1); B(2;1;1); C(1;2;-2); D(3;2;3)
Решение:
Сделаем схематический чертёж для решения задачи Рис 3.8
 |
|||
Рис 3.8
Найдём проекции векторов ![]()
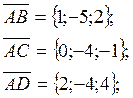
Из геометрического смысла
смешанного произведения известно, что 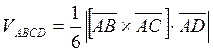 с
другой стороны объем пирамиды, как известно из школьного курса геометрии
с
другой стороны объем пирамиды, как известно из школьного курса геометрии 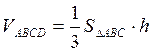
Но из геометрического смысла векторного произведения

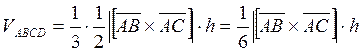 приравнивая
эти объекты, получим соотношение
приравнивая
эти объекты, получим соотношение 

Найдём смешанное
произведение векторов ![]()
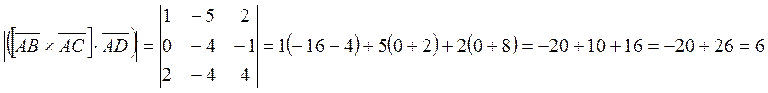
Найдём векторное
произведение ![]()
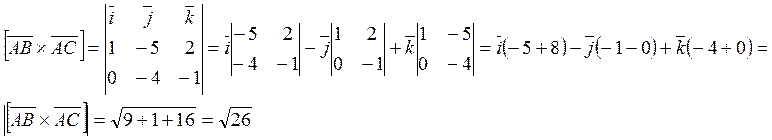

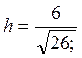
Задачи для самостоятельного решения
1.
Найти угол между векторами
![]() ;
;![]()
2.
Доказать, что ![]()
3. Определить синус угла А треугольника АВС с вершинами А(1,2,3); B(3,4,5); C(2,4,7)
4.
Доказать
перпендикулярность векторов ![]() и
и ![]()
5.
Найти проекцию вектора ![]() на направление вектора
на направление вектора ![]()
6.
Доказать, что вектор ![]() перпендикулярен вектору
перпендикулярен вектору ![]()
7.
Какой угол составляют
между собой два вектора 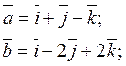
8.
Определить угол между
векторами ![]() и
и ![]() если
вектор
если
вектор ![]() перпендикулярен к вектору
перпендикулярен к вектору ![]() , а вектор
, а вектор ![]() перпендикулярен к вектору
перпендикулярен к вектору ![]()
9.
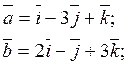 Найти площадь параллелограмма сторонами которого
являются векторы
Найти площадь параллелограмма сторонами которого
являются векторы
10.
Доказать, что векторы ![]()
![]()
![]() компланарны.
компланарны.
11. Вершины треугольной пирамиды находятся в точках A(0;0;0); B(3;4;-1); C(2;3;5); D(6;0;-3). Найти длину высоты пирамиды опущенной из вершины А.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.