Методы вычисления усилий в элементах фермы. Статические способы. Система уравнений равновесия всех узлов в статически определимой ферме

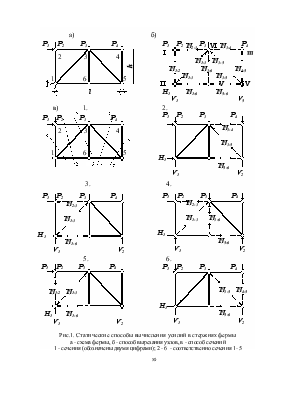
Обратим внимание на то, что во всех приведенных примерах имеются нулевые стержни (стержни с нулевыми усилиями). Если внимательно  просмотреть все решения, то можно установить несколько  простых  закономерностей, позволяющих определять нулевые стержни без вычислений. Это относится к следующим характерным узлам.

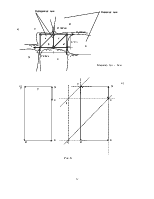
Незагруженный узел с двумя стержнями (рис. 2, а). Из уравнений равновесия следует:

                       S y = 0        fi N₁ = 0,

S x = 0        fi N₂ = 0.

Таким образом, из равновесия незагруженного узла  с  двумя  стержнями вытекает, что усилия в них равны нулю, то есть “оба стержня нулевые”.

Незагруженный узел с тремя стержнями, два из которых лежат  на одной прямой (рис.3, б). При составлении уравнений равновесия одну из осей (например, ось x) можно всегда направить перпендикулярно прямой,  на  которой  лежат два стержня. Тогда из уравнения

                            S x = 0        fi N₃ = 0.      

Значит,  если узел с тремя стержнями, два из которых лежат  на  одной прямой, не загружен, то усилие в  третьем  стержне  равно  нулю,  или третий стержень нулевой.

 5.2. Графический способ определения усилий в элементах фермы  Графический способ - это наглядная интерпретация метода  вырезания узлов. В нем используются графические приемы разложения и  суммирования сил (векторов),  которые  заменяют  процедуру  составления  и решения систем алгебраических уравнений. Инструментом при графическом расчете являются карандаш и линейка вместо технических средств вычислений,  применяемых  при  аналитическом  расчете.  При   аккуратности построений и  измерений  усилия,  полученные  графическим  способом, имеют достаточную для практических целей точность, а затрачиваемое на расчет время соизмеримо с расчетом на современных ЭВМ.

Разберем  графический  способ  на  примере.  Пусть  дана  ферма, загруженная сосредоточенными силами в узлах  (рис.  5.).  Опорные реакции будем считать известными. Таким  образом, к  ферме  приложена самоуравновешенная система сил.  Используем метод Кремоны –Максвелла.

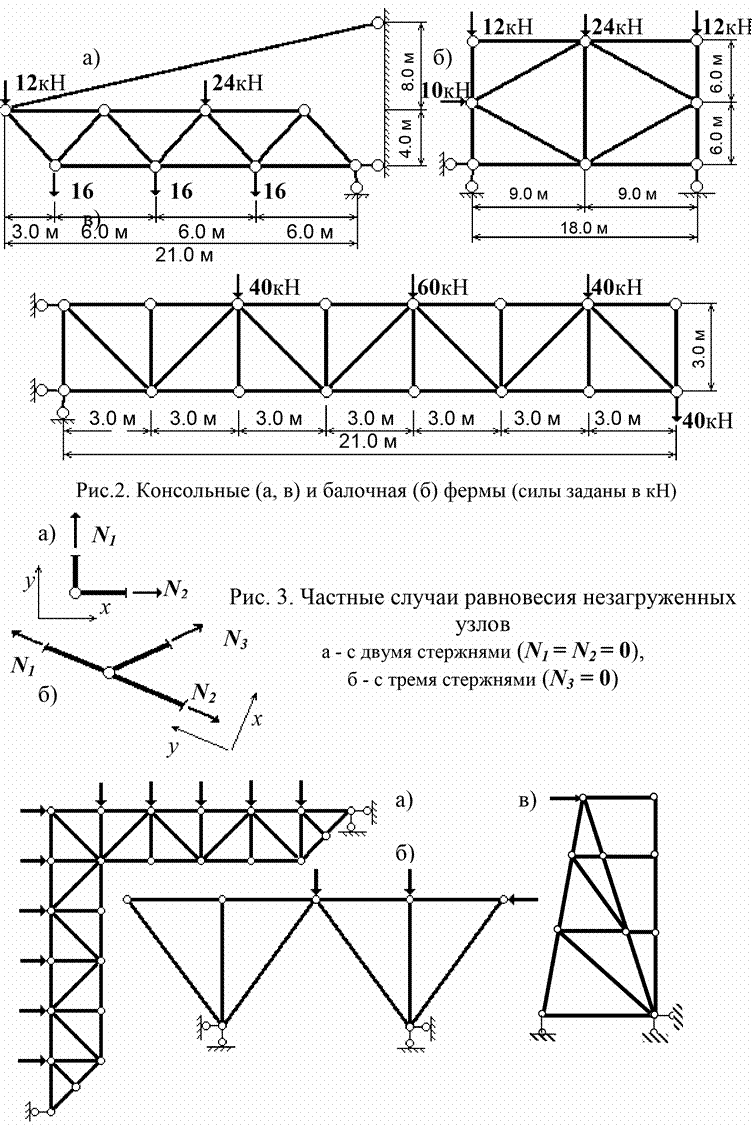Рис. 4. Рамная (а) , арочная (б) и балочная (в) фермы,     имеющие “нулевые“ стержни

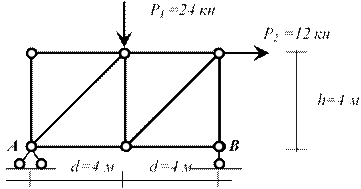
Рис. 5.

           Порядок построения диаграммы

Построение многоугольника внешних сил  

Обозначим внешние поля буквами  C, D, E, F и G.  Внешними полями называются области, ограниченные векторами внешних сил и элементами фермы

(см.рис.6, а).

Выбираем исходную точку отсчёта (любое поле, например С), масштаб  в 1см – 3 кн и строим многоугольник сил, обходя ферму по часовой стрелке. В масштабе откладываем величину внешних сил, которые при обходе пересекаем. В результате построения должен получиться замкнутый многоугольник (равнодействующая внешних сил равна нулю см. рис.6, б).

Построение многоугольника внутренних сил.

Обозначим внутренние поля буквами  a, b, c, d. Внутренними полями называются области, ограниченные элементами фермы.

Построение многоугольника внутренних сил начинаем с поля, которому принадлежит узел с  двумя элементами (например, поле а). Чтобы попасть в поле а из внешнего поля С необходимо  преодолеть вертикальный элемент А1 – проводим из точки С диаграммы линию, параллельную элементу А1(на чертеже – вертикальная пунктирная линия). Чтобы попасть в поле а из внешнего поля С также необходимо  преодолеть горизонтальный элемент 12 – проводим из точки С диаграммы линию, параллельную элементу 12 (горизонтальная пунктирная линия). Точка пересечения двух пунктиров будет точка а. Затем построим точку b – чтобы попасть в поле  b из поля а необходимо  преодолеть наклонный  элемент А2 – проводим из точки С диаграммы пунктирную линию, параллельную элементу А2 (на чертеже – наклонная пунктирная линия). Из точки F проводим горизонтальную пунктирную линию (параллельно элементу А4). Точка пересечения двух пунктиров будет точка  b.  Затем строим точки с и  d  . Причём, при построении точки  d  её положение можно проверить, так как она строится тремя линиями – используя поле E, F и с (рис.6, в).

Определение величины и знака усилия.

Для определения величины усилия в элементе 1-2 достаточно измерить длину отрезка С- а (элемент 1- 2 разделяет поля С и а). Усилие в этом элементе =0.

И так далее.

Для определения знака усилия необходимо узел обойти по часовой стрелке.

Например, определим знак усилия в элементе А-2 (рассмотрим узел А). При обходе узла по часовой стрелке, элемент А-2 лежит на границе полей а и b. Показываем направление на многоугольнике внутренних сил – из  a  в  b. Переносим это направление в узел А, получаем направление к узлу