Табличный расчёт изотропных плит. Схема плиты и действующие в ней усилия. Изгибающие моменты в единичной полоске плиты

         Лекция 6 

          Табличный расчёт изотропных плит

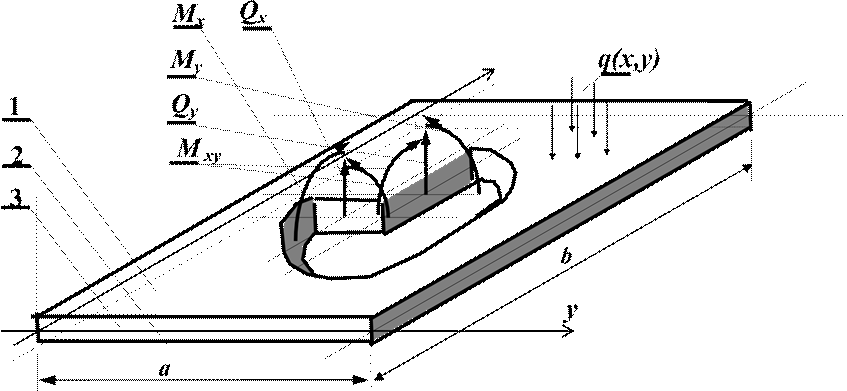
Для определения усилий в плитах используются  формулы,  в  которые входят безразмерные табличные множители (m_uv, d_uv, k, z) и размерные  величины для конкретной плиты (рис. 1, Способы опирания плит указаны в заголовках к таблицам):

         M_xi =m_xi K,  Q_xi  = d _xi K/b,   M_{кр  оп}   = z K,

 M_yi= m_yi  K,  Q_{y i}  =d _{y i}  K/a,   R  = r K,    w = kb² /D K, где M_xi , M_yi  - изгибающие моменты в сечениях проходящих через точку  i (номера точек указаны на схемах плит  к  таблицам) и перпендикулярных соответствующим осям; Q_xi  , Q_yi   - поперечные силы в тех же  сечениях; M_{кр оп} - крутящий момент в углах плиты; R - сосредоточенная реакция на опорах и в углах; x, y - прямоугольные координаты  срединной  поверхности; D = Eh³ /(12 (1-m ²)) - цилиндрическая жесткость плиты; E, n - модуль упругости и коэффициент Пуассона материала; h - толщина плиты; K = q a b - равнодействующая внешней нагрузки; a, b - размеры плиты в направлении  координатных осей x и y соответственно,  q  -  интенсивность равномерно распределенной нагрузки; m_xi  , m_yi  , d_xi  , d_yi, r, z, k  -  табличные коэффициенты, w - прогиб в середине плиты.

Таблицы составлены  на  основе  решения  уравнения  Софи  Жермен (6.1). По прогибам, получаемым из этого решения, вычисляются  усилия, например, 

          M_x =  D(д² w/дx² +  mд² w/дy²),                                     (6.1)           M_y =  D(д² w/дy² +  mд² w/дx²).

Из уравнений (6.1) следует,  что  усилия  зависят  от  значения коэффициента Пуассона m. В меньшей степени от него  зависят  прогибы, поперечные силы и реакции, но изгибающие и  крутящие  моменты  должны быть пересчитаны на заданный материал. Формулы  пересчета  получаются из уравнений (6.1) быть пересчитаны на заданный материал. Формулы  пересчета  получаются из уравнений (6.1)

 х

Рис. 1.   Схема плиты и действующие в ней усилия

1 - верхняя поверхность плиты,  2 - нижняя поверхность, 3 - срединная поверхность

M_x ⁼ 1-¹m ((1- mT m) M_xT + (m - mT ) M _yT )

             M _y ⁼ 1_-¹_m ((1- m_T m) M _yT + (m - m_T ) M_xT ) (6.2)

Mкр = 11--mm MкрT

где m_T , M_xT  ,  M_yT  ,  M_крT  -  табличные  значения или рассчитанные  с помощью  таблиц величины.

При определении усилий и перемещений ребристые  плиты,  а  также балочные клетки, часто заменяют эквивалентной плитой постоянной  толщины. Замена действительной конструкции эквивалентной пластиной неизбежно связана с неточностями при определении усилий и деформаций. Эти неточности тем больше, чем значительнее нарушения регулярности усилений. Толщина эквивалентной пластины h может быть принята  произвольно сообразно с удобством расчета, а модуль  упругости  E  и  коэффициент Пуассона m определяются заданной конструкцией

 E = E_к (А + h_к a)/(a h), m = m_к E_к /E,                   (6.3) где E_к , m_к , h_к - соответственно модуль упругости, коэффициент Пуассона и толщина плиты заданной конструкции, А - площадь поперечного  сечения ребер, a- расстояние между ними.

Р а с ч е т   п л и т   п о   т а б л и ц а м

П р и м е р  1. Определить усилия в свободно  опертой  плите, имеющей размеры в плане b = 1.8 м, a = 2.4 м, загруженной  равномерно распределенной нагрузкой q = 10 кН/м  (рис. 1).

Р е ш е н и е. Определим отношение b/a  =  1.8/2.4  =  0.75.  По таблице 1   найдем  безразмерные  коэффициенты  (так  как  в  таблице точного значения b/a = 0.75 нет, вычислим их линейной интерполяцией)

 m_x1  = 0.0306,  m_y1  = 0.0500,  m_x4  = 0.0203,  m_y4  = 0.0299,          m_x5  = 0.0224,  m_y5 = 0.0392,  m_x6  = 0.0278,  m_y6  = 0.0372,  d_x3 = 0,366, d_x8 = 0.299, d_y2  = 0.487, d_y7 =0.435, z= 0.0368.     

Значения изгибающих моментов, поперечных сил и крутящего момента в углах плиты получим для заданных  параметров  плиты  по   формулам, помещенным в начале таблицы. Тогда размерный множитель           K = q a b = 10 1.8 2.4 = 43.2 кН.

Величины усилий (изгибающих моментов в направлении оси x  и  оси y, поперечные силы в этих же направлениях и крутящий момент  в  углах плиты) будут соответственно равны:

         M_x1  = 0.0306 43.2 = 1.32 кНм/м,  M_y1 = 0.0500 43.2 = 2.16 кНм/м,

         M_x4  = 0.0203 43.2 = 0.88 кНм/м,  M_y4 = 0.0299 43.2 = 1.29 кНм/м,          M_x5  = 0.0224 43.2 = 0.97 кНм/м,  M_y5 = 0.0392 43.2 = 1.69 кНм/м,

         M_x6  = 0.0278 43.2 = 1.20 кНм/м,  M_y6 = 0.0372 43.2 = 1.61 кНм/м,

         Q_x3  = 0.366 43.2/1.8 =8.78 кН/м,  Q_y2  = 0.487 43.2/2.4 =8.77 кН/м,          Q_x8  = 0.299 43.2/1.8 =7.18 кН/м,  Q_y7  = 0.435 43.2/2.4 =7.83 кН/м,          M_{кр оп}   = 0.0368 43.2 = 1.59 кНм/м.

Имея в виду дополнительную  информацию,  вытекающую  из  условий закрепления, симметрии плиты  и  загружения,  а,  именно,  то  обстоятельство, что изгибающие моменты в направлении перпендикулярном  сторонам плиты при шарнирном закреплении равны нулю и поперечные силы на осях симметрии также нулевые, построим эпюры усилий (рис.1, б, в, г, д).

П р и м е р  10.10. Определить максимальные усилия  в  стержневой плите, состоящей из пентаэдров, представленной на рис. 2. Плита в плане имеет размеры 66 x 66 метров, опирание  на колонны - точечное. Нагрузка равномерно - распределенная, интенсивностью  q = 2.17 кН/м.

Р е ш е н и е. Соответственно отношению b/a = 1 (плита  квадратная в плане) и схеме опирания (см табл. 2) определяем безразмерные коэффициенты           m_x1  = 0.1049,  m_y1  = 0.1049, m_x2 = 0.1580,  m_y3  = 0.1580;

и размерный множитель