Формула
(14.4) имеет два неизвестных: требуемую площадь 
и
коэффициент продольного изгиба 
, который
является функцией гибкости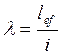 
, где lef
- расчетная длина стержня; i - радиус инерции сечения
стержня.
Задав
гибкость 
, по таблицам в нормах определяют
соответствующее значение и вычисляют
требуемую площадь.
Рекомендуемая
гибкость для поясов - 80
60, для
элементов решетки - 120100.
По заданной гибкости можно вычислить также и требуемые радиусы инерции
, 
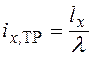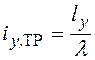, (14.5)
где 
и 
-
расчетные длины стержня соответственно в плоскости и из плоскости фермы,
определяются по таблицам норм проектирования.
В соответствии с требуемыми радиусами инерции и площадью сечения по сортаменту подбирается подходящий калибр профиля. Несовпадение табличных значений А и i с требуемыми указывает на то, что гибкость задана неудачно и требует корректировки.
Для подобранного сечения стержня необходимо выполнить проверку устойчивости. Вычисляют фактическую гибкость стержня в плоскости и из плоскости фермы:
, 
.
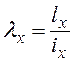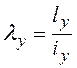Сечение стержня
считается оптимально скомпонованным, если выполняется условие равноустойчивости
- 
. Проверяют, чтобы максимальное
значение гибкости не превышало предельного значения: 
. Ограничение гибкости связано с
тем, что очень гибкие стержни легко искривляются от случайных воздействий,
которые могут иметь место при транспортировке или монтаже, вибрируют при
динамических нагрузках, провисают от собственного веса, в них появляются
нежелательные эксцентриситеты, ухудшающие условия работы стержня.
Нормами установлена предельная гибкость для сжатых поясов и опорных раскосов и стоек ферм 120, а для элементов решетки - 150.
По 
в таблице СНиПа определяют
соответствующие значения 
и выполняют проверку
по формуле:
.
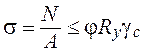2. Растянутые стержни
Требуемую площадь сечения нетто растянутого стержня определяют по формуле:
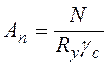. (14.6)
По требуемой площади назначают сечение и проверяют гибкость:
; 
.
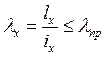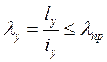Значение
предельной гибкости для растянутых поясов и опорных раскосов 
, для прочих растянутых элементов
ферм 
.
3. Подбор сечения по предельной гибкости
Некоторые стержни ферм имеют очень малые усилия, и подбор их по требуемой площади не представляется возможным. Такие стержни подбирают по предельной гибкости. Зная расчетную длину стержня и значение предельной гибкости, определяют требуемый радиус инерции:
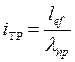. (14.7)
По радиусу инерции в сортаменте выбирают сечение, имеющее наименьшую площадь.
Стержни, в которых от разных сочетаний нагрузок возникают усилия разных знаков (растяжение и сжатие), следует рассчитывать на оба усилия и принимать большее из полученных сечений, а конструирование вести исходя из требований, предъявляемых к сжатым элементам.
Если за
основной критерий экономичности принимать минимум массы фермы, то каждый
стержень фермы должен иметь свое сечение, однако при этом резко возрастают
трудоемкость и стоимость изготовления. Поэтому количество типоразмеров сечений
обычно ограничивают: в фермах до 30 м - до шести, в фермах 3642 м - до восьми типоразмеров.
При этом в фермах пролетом до 24 м пояса обычно выполняют постоянного сечения,
рассчитанного по максимальному усилию в поясе. При бόльших пролетах сечение
пояса целесообразно изменять, но не более одного раза.
1. Назовите основной признак экономичного очертания фермы.
2. Как устанавливается оптимальная высота фермы?
3. Перечислите достоинства треугольной решетки.
4. В каких случаях целесообразно применять крестовую решетку?
5. С какой целью фермам придается строительный подъем и как назначает ся его величина?
6. Какие допущения приняты при статическом расчете ферм?
7. Назовите основное достоинство ферм из замкнутых профилей.
8. По каким геометрическим параметрам подбирают сечение сжатого
стержня фермы?
9. Почему накладываются ограничения на гибкость растянутых стержней?
10. В чем заключается расчет стержня по предельной гибкости?
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.