Построение графиков, поверхностей и решение нелинейных уравнений средствами электронной таблицы excel

решения задачи нам потребуется использовать логическую функцию ЕСЛИ. 

Функция ЕСЛИ используется для условной проверки значений и формул. Она возвращает одно значение, если заданное условие при вычислении дает значение ИСТИНА, и другое значение, если ЛОЖЬ.

Синтаксис логической функции ЕСЛИ

ЕСЛИ(лог_выражение;значение_если_истина;значение_если_ложь) Лог_выражение   - это любое значение или выражение, которое при вычислении дает значение ИСТИНА или ЛОЖЬ.

Значение_если_истина   - это значение, которое возвращается, если лог_выражение имеет значение ИСТИНА. Если лог_выражение имеет значение ИСТИНА и значение_если_истина опущено, то возвращается значение ИСТИНА. Значение_если_истина может быть другой формулой.

Значение_если_ложь   - это значение, которое возвращается, если лог_выражение имеет значение ЛОЖЬ. Если лог_выражение имеет значение ЛОЖЬ и значение_если_ложь опущено, то возвращается значение ЛОЖЬ. Значение_если_ложь может быть другой формулой.

ЗАМЕЧАНИЯ

•До 7 функций ЕСЛИ могут быть вложены друг в друга в качестве значений аргументов значение_если_истина и значение_если_ложь, что позволяет конструировать более сложные проверки.

•Функция ЕСЛИ всегда возвращает значение, возвращаемое вычисленным аргументом значение_если_истина и значение_если_ложь.

•Если какой-либо аргумент функции ЕСЛИ является массивом, то при выполнении функции ЕСЛИ вычисляется каждый элемент массива. Если какой-либо из аргументов значение_если_истина или значение_если_ложь является действием, то все действия выполняются.

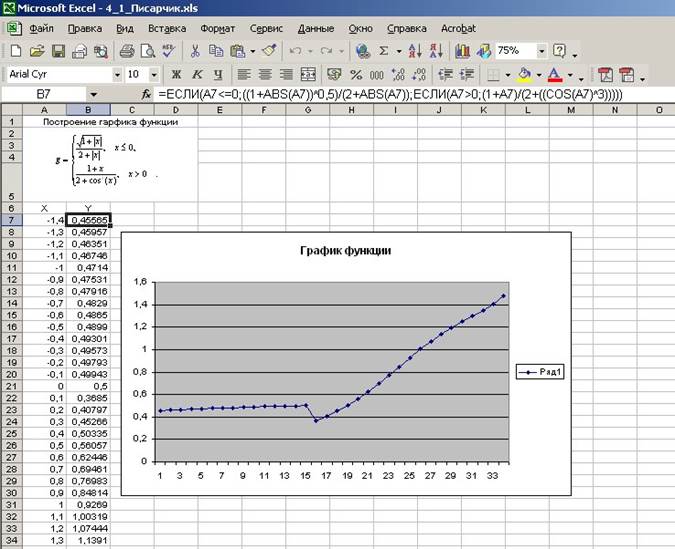
            Введем в ячейку В7 формулу:

=ЕСЛИ(A7<=0;((1+ABS(A7))^0,5)/(2+ABS(A7));ЕСЛИ(A7>0;(1+A7)/ (2+((COS(A7)^3)))))

Установим указатель мыши на маркере заполнения как показано на рис. 1.5 и удерживая левую кнопку мыши протаскиваем его вниз до тех пор, пока не получится числовой ряд нужной длины, т.е. вниз до ячейки В40 (включительно). 

Построим график, используя те же действия как и в предыдущем случае.

Результат вычислений и построения графика показан на рисунке

1.12.

Рис. 1.12. Вид листа рабочей книги после построения  графика функции



                                                                                                                                                 ,

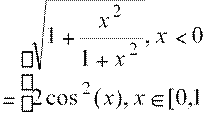
                  Построим теперь график функцииz                     ₁₃ ,],x_>1.

_ 1₊ 2sin(3x)





Для построения графика функции необходимо сначала построить таблицу ее значений при различных значениях аргумента. Выбираем шаг изменения аргумента равный 0.2. В ячейки А41:А56 вводим значения переменной x: -1.5, -1.3, -1.1, …,1.5. Для получения значений функции в ячейку В41 введем формулу:

=ЕСЛИ(A41<0;КОРЕНЬ(1+A41^2*(1+A41^2));ЕСЛИ(И(A41>=0;A41<=1); 2*COS(A41)^2;КОРЕНЬ(1+ABS(2*SIN(3*A41))^(1/3))))

Использование встроенной функции ЕСЛИ совместно с функцией И позволяет нам произвести вычисление значений функции z для трех поддиапазонов значений аргумента.

Чтобы вычислить значения функции при всех аргументах, выделим ячейку В41, установим указатель мыши на маркере заполнения этой ячейки (маркер приобретает вид крестика в нижнем правом углу ячейки) и протаскиваем его вниз до ячейки В56 (рис.1.13).

Для построения графика функции выделим ячейки А41:В56 и вызовем мастер построения диаграмм Вставка-Диаграмма. Далее выбираем вид диаграммы – Гладкие графики. Нажимаем кнопку «Далее». На закладке «Ряд» убираем аргумент из списка рядов, т.е. оставляем только функцию. В окно «Подписи оси X» вводим диапазон ячеек для аргумента «=a!$A$41:$A$56». Нажимаем кнопку «Далее». На закладке «Легенда» убираем птичку в окне «Добавить легенду». На закладке «Заголовки» вводим название графика – «График функции z», название оси х – «Х», название оси y – «Y». Нажимаем кнопку «Далее», затем – «Готово». После этого растягиваем область диаграммы до нужного размера

(рис.1.13).

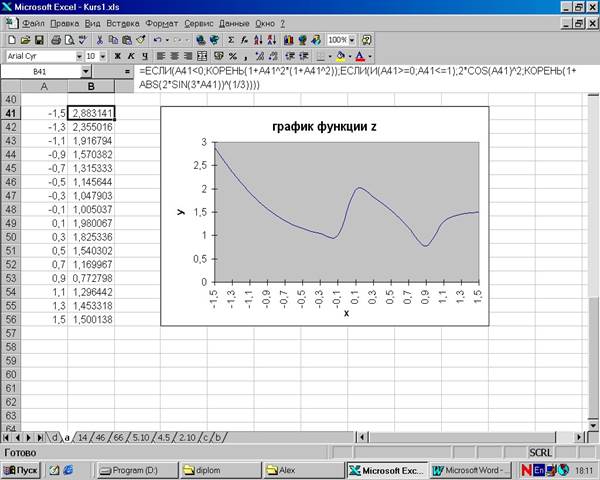
Рис.1.13.  Вид листа рабочей книги после построения  графика функции

ЗАДАЧА 2

Построить в одной системе координат при x∈[−1,8; 2,7] графики следующих двух функций: y = 2sin(2πx)⋅cos(4πx),

z = cos²(3πx)− cos( )πx ⋅sin( )πx .

Решение

Для построения графиков функций необходимо сначала построить таблицу их значений при различных значениях аргумента, причем аргумент в нашем случае для двух функций пусть изменяется с фиксированным шагом, например,  0,2. Выбор этого шага обусловлен необходимостью более наглядного отображения значения функции на интервале табуляции, т.е на интервале от минус 1,8 до 2,7.

            Создадим в Excel таблицу следующего вида (рис. 1.14).

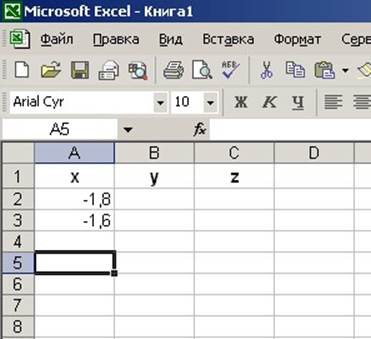
Рис. 1.14. Ввод исходных данных

Зафиксируем курсор в ячейке А2 и выберем команду Правка⇒Запольнить⇒Прогрессия (рис.1.15). После ее выполнения появится диалоговое окно Прогрессия