Знакопеременные ряды. Разграничение на абсолютную и условную сходимости рядов

Сходимость и сумма ряда (1) определяются как и ранее.  

Рассмотрим ряд, составленный из абсолютных величин

∞

членов ряда:     ∑| a_n |               (2)

n=1

Док-во. Пусть  a_n =| a_n | +a_n ≥ 0   и   b_n =| a_n | −a_n ≥ 0   Ряды     —  знакоположительны    и так

как a_n < 2a_n,  b_n < 2a_n(!), то по признаку сравнения они

aⁿ −bⁿ  и по свойству суммы сходятся. Но  a_n =

2  ∞

сходящихся рядов получаем, что ряд ∑a_n  сходиться

n=1 cosα cos2α  cosnα

Пример. Исследовать              +           +...   +...

3  3        3

                                                                                           1            2                n

Решение. Данный ряд является знакопеременным.

Составим ряд из абсолютных величин данного ряда:

                                                 cosα     cos2α        cosnα

                                                                     +                  ...++…   .

                                                         3                   3                        3

                                                      1             2                 n

                                                   1      1             1

членов ряда        +     +...+            +..., который сходится, как

                                                 13      23               n3

обобщенный гармонический ряд 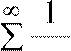 ,  где  p >1.

p

n=1n

Значит, по теореме Коши, исходный ряд сходится. 

Замечание. Разграничение на абсолютную и условную сходимости рядов весьма существенно. Оказывается, что некоторые свойства конечных сумм переносятся только на абсолютно сходящиеся ряды; условно сходящиеся ряды такими свойствами не обладают. 

Некоторые свойства абсолютно сходящихся рядов:

1) Любая перестановка членов абсолютно сходящегося ряда приводит к  абсолютно сходящемуся ряду с той же суммой; перестановкой же  членов условно сходящегося ряда можно получить любую наперед заданную сумму

(теорема Римана).

Пример.   Рассмотрим условно сходящийся ряд

1− 1 + 1 − 1 + 1 − 1 + 1 − 1...+(−1)^{n+1 1} +...  (А)

                                    2      3    4    5    6    7    8                    n

Переставим его члены так, чтобы после каждого положительного стояли два отрицательных:

1−  −......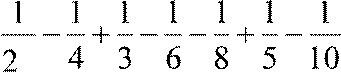

Сложим каждый положительный член с одним отрицательным:             ...+...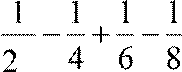

Получили в итоге  ряд (А), все члены которого умножены на число . По свойству сходящихся рядов (умножение на постоянную!) полученный ряд также сходится и его сумма равна S. Таким образом, перестановка членов ряда уменьшила сумму условно сходящегося ряда в два раза.

Знакочередующиеся ряды. Признак Лейбница

Укажем простой достаточный признак сходимости знакочередующегося ряда.

Теорема                (признак Лейбница).    Если для  знакочередующегося ряда 

a₁ − a₂ + a₃ −...(−1⁾ⁿ⁻¹+… , a_n > 0 выполняются условия: 1) a₁ >a₂ > ... >a_n > ...;  2) lim a_n = 0, 

n→∞

то ряд сходится и его сумма  не превосходит первого члена ряда 0 < S < a₁, а остаток ряда r_n  не превышает по абсолютной величине первого отбрасываемого члена:    r_n <a_n+1.

(Ряды, удовлетворяющие условиям теоремы, иногда называют рядами Лейбница)

Док-во. Запишем частичную сумму S_2m четного числа членов ряда в виде 

S2m = (a1 − a2 )+ (a3 − a4 )+...+(a2m−1 − a2m)    

Так как    (a₁ − a₂ ) > 0,....,(a_2m−1 − a_2m) > 0, то S_2m > 0 для любого m.  Кроме того, эта частичная сумма монотонно возрастает с ростом m. С другой стороны частичную сумму (В)    можно переписать в виде        S_2m = −a₁ −(a₂ − a₃) −(a₄ − a₅)−...− a_2m)

Очевидно, сумма     S_2m < a₁ и  убывает с ростом m.

Объединяя два неравенства, получим 0 < S_2m < a₁

Итак, имеем последовательность, которая монотонно возрастает и ограничена сверху⇒она сходится  limS_2m = S.

Так как S_2m+1 = S_2m + a_2m+1, то для частичных сумм с нечетным числом членов ряда имеем

lim S2m+1 = lim S2m + lim a2m+1 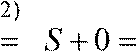  S .

m→∞                      m→∞               m→∞

Итак, ряд сходится и его сумма удовлетворяет неравенству   | S |< a₁. 

Оценим теперь остаток ряда, который запишем в виде

rn = (−1)n(an+1 −an+2 + an+3 +......)

Это опять знакочередующийся ряд. Значит для него верны доказанные выше оценки. 

Исследовать ряд           1−

Решение. Данный ряд – знакочередующийся. Члены его

1  1

убывают по абсолютной величине : 1>    > ... >                                                              > ....   

2  n

1

и предел общего члена lim    = 0. 

n→∞ n

Следовательно, этот ряд сходится и его сумма S ≤1.

Однако ряд, составленный из абсолютных величин

1+ 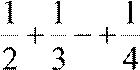 +... (гармонический ряд)

является расходящимся, т.е. исходный ряд является условно (неабсолютно) сходящимся.

Для математического анализа в первую очередь нужны функциональные ряды, т.е. ряды, членами которых являются функции. Наиболее важным для приложений является специальный класс функциональных рядов ― степенные ряды.