Язык — это множество строк, которые могут быть сгенерированы некоторым деревом разбора. Процесс поиска дерева разбора для данной строки терминалов называется разбором или синтаксическим анализом этой строки.
Пример 3. Вывод 9-5+2 в грамматике примера 1
показан деревом:
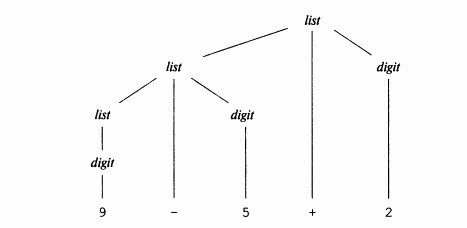
Рис. Дерево разбора строки 9-5+2 в соответствии с грамматикой примера 1.
list list + digit — продукция грамматики примера 1. Левый дочерний узел корня аналогичен корню, только его дочерний узел помечен как – вместо +, все узлы, помеченные как digit имеют по одному дочернему узлу с метками-цифрами. Листьями является строка 9-5+2
Пример 4. Синтаксические деревья позволяют
моделировать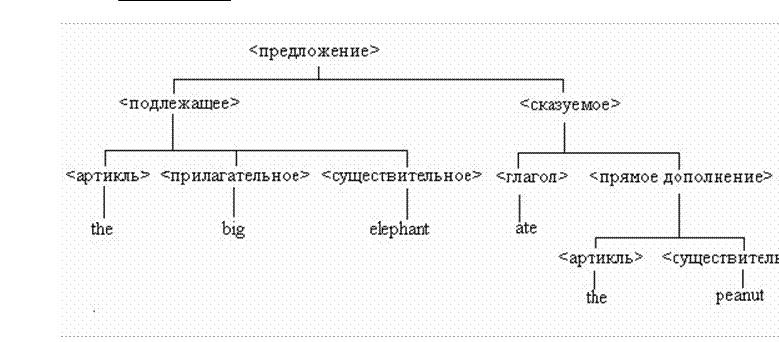 
синтаксические структуры предложений
естественного языка:
§ Для каждого синтаксического дерева существует, по крайней мере, один вывод.
§ Для каждого вывода есть соответствующее синтаксическое дерево (но несколько выводов могут иметь одно и то же дерево).
§ Каждый узел дерева помечен символом грамматики. Каждый внутренний узел и его дочерние узлы соответствуют продукции: внутренний узел соответствует заголовку продукции, а дочерни узлы — телу продукции.
§ Концевые узлы дерева образуют выводимую сентенциальную форму.
Грамматика может иметь более одного дерева разбора для данной строки терминалов.
Такая грамматика называется неоднозначной.
КС-грамматика G называется неоднозначной, если существует хотя бы одна цепочка L (G), для которой может быть построено два или более различных деревьев вывода.
Это утверждение эквивалентно тому, что цепочка имеет два или более разных левосторонних (или правосторонних) вывода.
В противном случае грамматика называется однозначной.
Язык, порождаемый грамматикой, называется неоднозначным, если он не может быть порожден никакой однозначной грамматикой.
Чтобы показать неоднозначность грамматики, достаточно найти строку терминалов, которая дает более одного дерева разбора.
Неоднозначность грамматики — это свойство грамматики, а не языка. Т.е. для некоторых неоднозначных грамматик существует эквивалентные им однозначные грамматики.
Если грамматика используется для определения языка программирования, то она должна быть однозначной.
Пример 5 неоднозначной грамматики G=({if, then, else, a, b}, {S}, P, S), где P
= { S if b then S else S| if b then S | a}.
В этой грамматике для цепочки if then if then a else a можно построить два различных вывода.
Разные деревья вывода предполагают соответствие else разным then. Если договориться, что else должно соответствовать ближайшему к нему then, и подправить грамматику G, то неоднозначность будет устранена:
S if b then S| if b then S’ else S | a
S’ if b then S’ else S’| a
Пример 6 Если в примере 1 использовать только
один нетерминал string, то грамматику можно записать: string string + string | string –
string|0|1|2|3|4|5|6|7|8|9
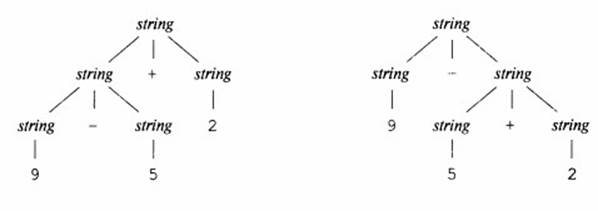
Объединение записей для digit и list имеет кажущийся смысл, т.к. отдельная цифра является частным случаем списка. Но при этом, например, для выражения 9-5+2, в такой грамматике существует больше одного дерева разбора Эти два дерева разбора соответствуют двум вариантам расстановки скобок в выражении: (9-5)+2 и 9-(5+2). Второе выражение дает в результате значение 2 вместо 6. Грамматика примера 1 не допускает такой интерпретации.
Дерево вывода можно строить нисходящим либо восходящим способом.
При нисходящем разборе дерево вывода формируется от корня к листьям; на каждом шаге для вершины, помеченной нетерминальным символом, пытаются найти такое правило вывода, чтобы имеющиеся в нем терминальные символы «проектировались» на символы исходной цепочки.
Метод восходящего разбора заключается в том, чтобы исходную цепочку сворачивают к начальному символу S; на каждом шаге ищется подцепочка, которая совпадает с правой частью какого –либо правила вывода; если такая подцепочка находится, то она заменяется нетерминалом из левой части этого правила.
Если грамматика однозначная, то при любом способе построения будет получено одно и то же дерево разбора.
По соглашению 9+5+2 эквивалентно (9+5)+2, а 9-5-2 эквивалентно (9-5)-2. Когда операнд типа 5 имеет операторы и слева, и справа, необходимы
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.