Статистическое изучение динамики социально-экономических явлений. Виды представления: таблици и графики

Средний уровень ряда для моментных рядов (как средняя хронологическая простая или взвешенная):  ,  .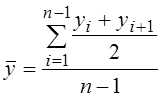

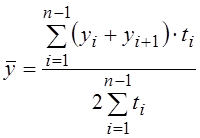Средний абсолютный прирост  ,   .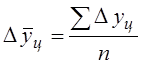

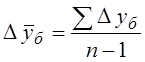Средний коэффициент роста  .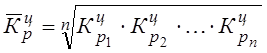

Средний темп роста   .

Средний темп прироста   .

Коэффициент опережения  .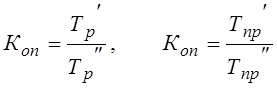

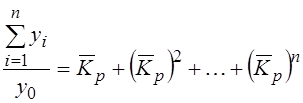 – средняя параболическая формула  предложена в 1975 г. проф. Л.С.Казинцом.

Проверка гипотезы о существовании тенденции

Ряд динамики разбивается на две равные или почти равные части. Проверяется гипотеза о существовании разности средних: . Для малых выборок за основу проверки берется  – критерий Стьюдента. При  гипотеза об отсутствии тренда отвергается, при  гипотеза принимается. В случае равенства или при несущественном различии дисперсий двух исследуемых совокупностей  исчисляется отношение средних с помощью выражения: 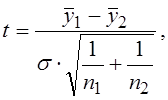   где  – средние для первой и второй половины ряда динамики,  – число наблюдений в этих частях ряда,  – среднее квадратическое отклонение разности средних.

Значение  берется с числом степеней свободы равным . Необходимое значение  можно определить на основе средней взвешенной величины дисперсий отдельных совокупностей:

.

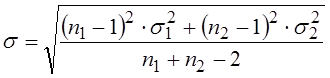При оценивании дисперсий для первой и второй частей ряда динамики возьмем число степеней свободы, соответственно равное :

.

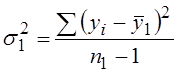Проверка гипотезы о равенстве дисперсий реализуется с помощью F–критерия, который основан на сравнении расчетного отношения с табличным:

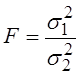, где .

Если расчетное значение F меньше, чем табличное, при заданном уровне вероятности , то можно принять гипотезу о равенстве дисперсий. Если же F больше, чем табличное значение, то гипотеза о равенстве дисперсий отклоняется, и, следовательно, формула 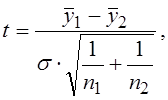 для испытания разности средних не может быть применена.

Данный метод дает вполне приемлемые результаты лишь в случае рядов с монотонной тенденцией.

Методы анализа основной тенденции (тренда) в рядах динамики

Основной тенденцией развития (трендом) называется плавное и устойчивое изменение уровня явления во времени, свободное от случайных колебаний.

Метод усреднения по левой и правой половине. Разделяют ряд динамики на примерно равные части, находят для каждой из них среднее арифметическое значение и проводят через полученные точки линию тренда на графике.

Метод укрупнения интервалов. Ряд динамики разбивается на две равные или почти равные части. Проверяется гипотеза о существовании разности средних: . Для малых выборок за основу проверки берется  – критерий Стьюдента.

Метод скользящей средней.

Пример. Исходные данные и результаты расчета скользящей средней, ц/га

При сглаживании по четному числу уровней значение скользящей средней относится к промежутку между временными точками, тогда из каждой пары смежных промежуточных значений скользящих средних находят среднюю арифметическую, которую и относят к определенной дате (периоду). Такой прием двойного расчета сглаженных уровней называется центрированием.

Метод аналитического выравнивания.

1.  определение на основе фактических данных вида гипотетической функции , способной наиболее адекватно отразить тенденцию развития исследуемого показателя;

2.  нахождение по эмпирическим данным параметров указанной функции;

3.  расчет по найденному уравнению теоретических (выровненных) уровней.

Правила:

1.  выравнивание по прямой линии, если абсолютные приросты более или менее постоянны;

2.  выравнивание по параболе второго порядка, если ускорения более или менее постоянны;

3.  выравнивание по показательной функции, если значения уровней меняются в геометрической прогрессии, т.е. цепные коэффициенты роста более или менее постоянны;

4.  выравнивание по гиперболе, если обнаружена тенденция замедленного снижения уровней ряда.

См. системы нормальных уравнений, полученных методом наименьших квадратов:

1)  для линейной зависимости:  

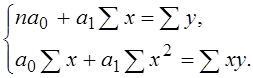
2)  для параболической зависимости:

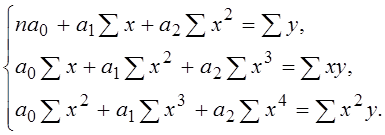
или: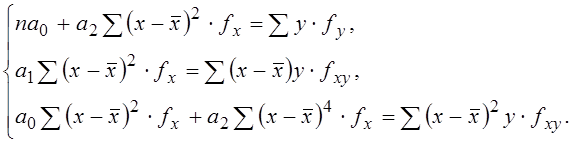

3)  для показательной зависимости:

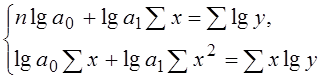
4)  для гиперболической зависимости:

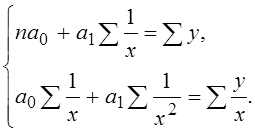
Для нашего примера изменения урожайности по годам: пусть . Тогда система нормальных уравнений имеет вид:

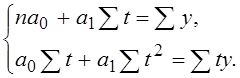
При четном числе уровней значения t – условное обозначение времени:

1995               1996                1997                1998                1999                2000

-5                    -3                     -1                     +1                   +3                    +5

При нечетном числе уровней значения t устанавливаются по-другому: