Пусть задано некоторое множество X элементов произвольной природы. Всякое отображение f: N → X множества натуральных чисел N в заданное множество X называется последовательностью (элементов множества X).
Образ натурального числа n, а именно, элемент xn = f (n), называется
n-ым членом или элементом последовательности, а порядковый номер члена последовательности – ее индексом.
Связанные определения
1) Подмножество f (N) множества X, которое образовано элементами последовательности, называется носителем последовательности: пока индекс пробегает множество натуральных чисел, точка, «изображающая» последовательность, «перемещается» по носителю.
2) Если взять возрастающую последовательность натуральных чисел, то её можно рассматривать как последовательность индексов некоторой последовательности: если взять элементы исходной последовательности с соответствующими индексами (взятыми из возрастающей последовательности натуральных чисел), то можно снова получить последовательность, которая называется подпоследовательностью заданной последовательности.
Комментарии
1) Не следует смешивать носитель последовательности и саму последовательность. Например, точка a є X как одноточечное подмножество {a} є X является носителем стационарной последовательности вида a, a, a, a, …
2) Любое отображение множества N в себя также является последовательностью.
Обозначения
Последовательности вида
x1 , x2 , x3 , …
принято записывать при помощи круглых скобок:
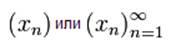
Иногда используют фигурные скобки:
Предел последовательности
Определение 1: Последовательность {хп}
называется ограниченной сверху (снизу), если существует такое число М (m), что для любого элемента этой
последовательности имеет место неравенство 
, при этом число М (m) называют верхней
(нижней) гранью.
Определение 2: Последовательность {хп} называется ограниченной, если она ограничена и сверху, и снизу, т.е. существуют М, m, что для любого
xn є {xn} следует, что m≤ xn ≤ M.
Обозначим
А = max {|M|, |m|}, тогда очевидно, что
последовательность будет ограничена, если для любого 
выполняется равенство |xn|≤А, последнее
неравенство есть условие ограниченности последовательности.
Определение
3: Последовательность 
называется
бесконечно большой последовательностью, если для любого А>0, можно указать
такой номер N, что для всех n>N выполняется ||>A.
Определение 4: Последовательность {αn} называется бесконечно малой последовательностью, если для любого наперёд заданного ε > 0, можно указать такой номер N(ε), что для любого n > N(ε) будет выполняться неравенство | αn | < ε.
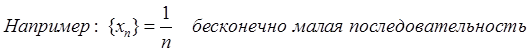
Определение 5: Последовательность {хп} называется сходящейся, если существует такое число а, что последовательность {хп – а} является бесконечно малой последовательностью. При этом само а – предел исходной числовой последовательности.
Из этого определения следует, что все бесконечно малые последовательности являются сходящимися и предел этих последовательностей = 0.
В связи с тем, что понятие сходящейся последовательности увязано с понятием бесконечно малой последовательности, то определение сходящейся последовательности можно дать в другой форме:
Определение 6: Последовательность {хп}
называется сходящейся к числу а, если для любого сколь угодно малого 
найдётся такой 
, что для всех n > N выполняется неравенство 
при 
,
Где а – предел последовательности
Т.к. равносильно 
, а это означает принадлежность интервалу хn є (a – ε; a+ ε) или, что то же самое, принадлежит ε – окрестности точки а.
Тогда мы можем дать ещё одно определение сходящейся последовательности.
Определение 7: Последовательность {хп} называется сходящейся, если существует такая точка а, что в любой достаточно малой ε – окрестности этой точки находится сколь угодно элементов этой последовательности, начиная с некоторого номера N.
Замечание: согласно определениям (5) и (6), если а – предел последовательности {хп}, то xп – а является элементом бесконечно малой последовательности, т.е. xп – а = αn, где αn – элемент бесконечно малой последовательности. Следовательно, xп = а +αn, и тогда мы в праве утверждать, что если последовательность {хп} сходится, то её всегда можно представить в виде суммы своего предела и элемента бесконечно малой последовательности.
Верно и обратное утверждение: если любой элемент последовательности {хп} можно представить в виде суммы постоянного числа и элемента бесконечно малой последовательности, то это постоянная и есть предел данной последовательности.
Характерные примеры нахождения пределов последовательности
Числовая последовательность задана общим членом xп, рассмотрим его:
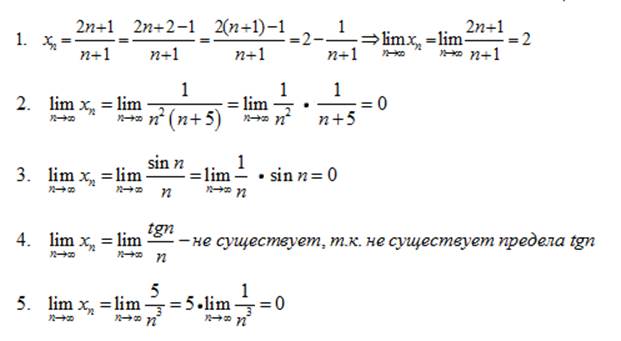
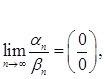
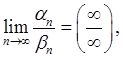при нахождении такого предела говорят, что будем раскрывать
неопределённость вида 
.
при нахождении такого предела,
говорят, что будем раскрывать неопределенность вида 
.
Для
раскрытия неопределённости доделим
числитель и знаменатель на наибольшую степень n.
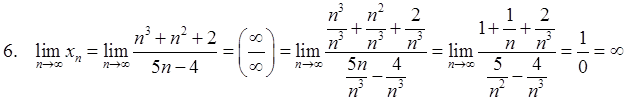
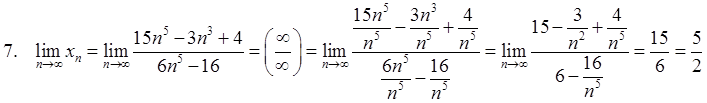
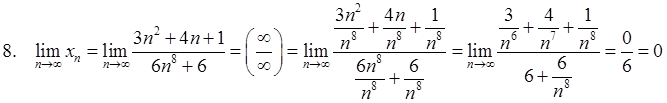
Таким образом, имеет место правило:
Предел отношения двух многочленов равен бесконечности, если степень числителя больше степени знаменателя, нулю, если степень числителя меньше степени знаменателя и отношению коэффициентов при старших членах, если степени числителя и знаменателя равны.
9. Пусть дана сходящаяся последовательность {хn} и пусть lim хn = a.
n→∞
Возьмем, например, ε=1. Согласно определению предела последовательности, существует такое n1, что для всех n > n1 выполняется неравенство | хn – a| < 1. Пусть d – наибольшее из чисел 1, | х1 – a|, …, | хn1 – a|. Тогда для всех n=1, 2, … справедливо неравенство | хn – a| ≤ d, т.е. для всех n
a – d ≤ хn ≤ a + d
Это означает ограниченность заданной последовательности.
Заключение
В данной работе мы определили понятие метрического пространства
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.