Этап функционального проектирования. Методы оптимизации. Особенности системного уровня, страница 3

Основная проблема постановки задачи оптимизации – формулирование целевой функции. В первую очередь это связано с тем, что вектор выходных параметров проектируемой ТС не может выступать в качестве целевой функции, поскольку, в силу функциональной зависимости выходных параметров от входных, невозможно улучшение всех выходных параметров одновременно, независимо друг от друга в процессе решения задачи оптимизации.

Если среди выходных параметров можно выделить один, наиважнейший, который максимально характеризует свойства объекта, то его принимают в качестве целевой функции. При этом остальные выходные параметры относятся к ограничениям в виде соответствующих условий работоспособности. Такой выбор целевой функции лежит в основе критериев оптимальности, которые называют частичными критериями.

Например, при расчетах металлоконструкций в качестве целевой функции принимают или запас прочности, или запас стойкости. Остальные условия работоспособности относятся к ограничениям задачи.

Как видим, задача оптимизации является сложной, многоплановой проблемой. Перейдем теперь к методам ее решения. Их рассмотрение проведем на базе математической постановки задачи однокритериальной оптимизации.

Пусть заданы:

1)  f(x) – целевая функция (функция эффективности), определяющая степень эффективности в достижении определенной цели;

2)  х – множество возможных решений (управляющих параметров);

3)  хÎРÌRⁿ – система ограничений (система условий задачи).

Необходимо определить значение х^*, которое удовлетворяет условиям (ограничениям) задачи, при котором целевая функция f(x) принимает экстремальное значение: f(x)®min или f(x)®mах.

Если в задаче оптимизации вместо ограничения общего вида хÎРÌRⁿ рассматривается отдельный вид ограничения, а именно: g_i(x)=0, i=1, …, m, xÎP, то имеем так называемую классическую задачу на условный экстремум.

Если вместо этого рассматривают следующий отдельный вид ограничений: g_i(x)<=0, i=1, …, k; g_i(x)=0, i=k+1, …, m, xÎP; x_i>b_i, i=1, …, m, то имеем так называемую задачу математического программирования.

При классификации задач однокритериальной оптимизации в такой общей математической постановке критерием классификации может выступать любой математический объект:

• функция f(x);
• управляющие переменные х;
• ограничения g_i(x).

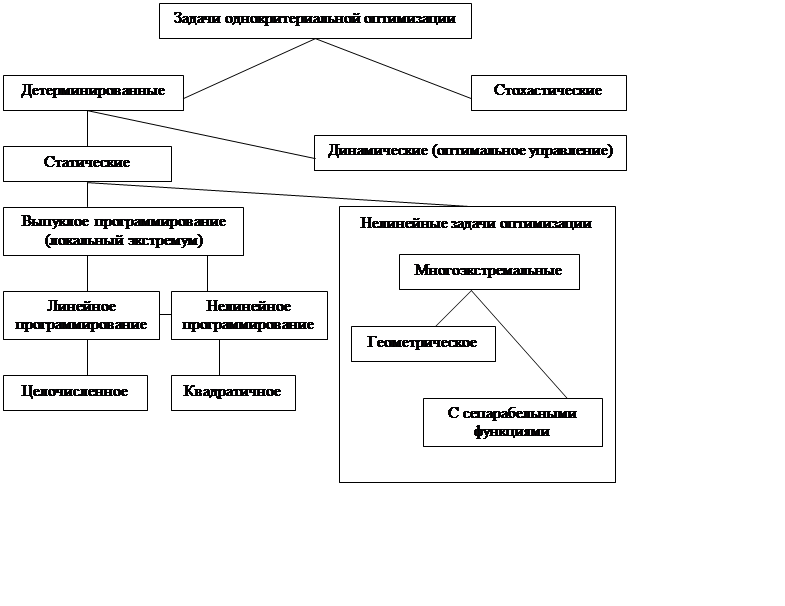
Учитывая это, можно провести следующую классификацию задач оптимизации (рис.2).

Если в качестве критерия классификации выбрать характер управляющих переменных, который отражает их вероятное поведение или детерминированные свойства, то задачи оптимизации можно разбить на две группы – детерминированные и стохастические.

Если в качестве критерия классификации выбрать систему ограничений, то задачи оптимизации разбивают на классы: условной и безусловной.

Если решение х^* задачи оптимизации является функцией времени х(t), то приходим к классу задач оптимизации динамических систем. Если критерием оптимальности является некоторый функционал, приходим к так называемым задачам оптимального управления. Задачи, не относящиеся к этому классу, условно назовем статическими. Группа детерминированных статических задач разбивается на одно-экстремальные (задачи выпуклого программирования) и многоэкстремальные.

В зависимости от вида функции f(x) каждая из этих групп разделяется на соответствующие задачи, такие как линейного программирования, нелинейного программирования и т.п.

В конце концов, в задаче оптимизации указанные виды множеств допустимых значений могут состоять из непрерывных или дискретных величин. В последнем случае приходим к задаче дискретной оптимизации, такой, например, может быть задача линейного целочисленного программирования.

Рисунок 1 - Структурно-функциональная схема системы электроснабжения

Рисунок 2 – Классификация задач оптимизации